Usando coordenadas polares no plano () e a definição de cônica dada por 11.7.4, parte 3, você pode deduzir de modo simples as equações polares das cônicas, tomando o pólo no foco e o eixo polar e o eixo polar e sua extensão ao longo do eixo principal.
a) Mostre que nestas condições a equação polar das cônicas é dada por
(O sinal ou é dado conforme a diretriz correspondente ao foco no pólo esteja à esquerda ou à direita deste.)
b) Dê exemplos de elipses, parábolas e hipérboles com suas formas polares.
c) Um cometa está se movendo em uma órbita parabólica em torno do Sol no foco da parábola. Faz-se uma observação do cometa quando ele está no ponto a 15 milhões de quilômetros do Sol; uma segunda observação é feita quando ele está no ponto a 5 milhões de quilômetros do Sol.
O segmentos de reta e são perpendiculares. Com estas informações há duas órbitas possíveis para o cometa. Encontre a distância mais próxima que o cometa passa do Sol, em cada órbita.
d) A órbita do planeta Mercúrio em torno do Sol é elíptica, com o Sol em um dos focos, tendo o semi-eixo maior 36 milhões de quilômetros e excentricidade . Encontre: (a) qual é a distância mais próxima que Mercúrio passa do Sol e (b) a maior distância possível entre Mercúrio e o Sol.
Passo 1
Vamos considerar primeiro a situação em que a reta diretriz está à direita do foco:
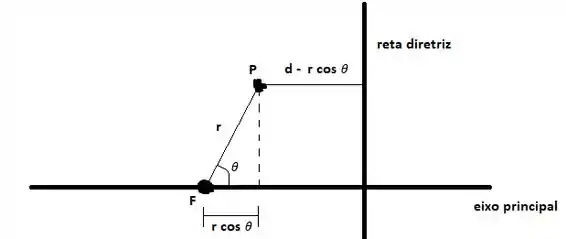
A condição que os ponto devem satisfazer para estar na cônica é
Nessa expressão, é a distância entre os pontos e ; é a distância do ponto à reta diretriz e é a excentricidade. Essa é a definição dada pela 11.7.4, parte 3:
Com isso, podemos escrever
Logo,
Portanto,
Caso a diretriz esteja à esquerda do foco, a única diferença é
Com isso nós provamos o que foi pedido no item (a).
Passo 2
Agora temos que dar alguns exemplos de cônicas em coordenadas polares. Por simplicidade vou escolher casos com .
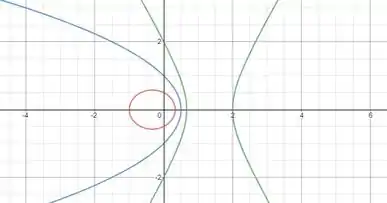
Para , temos uma elipse. Já para obtemos uma párabol e para obtemos uma hipérbole. A seguir temos as curvas para e quando a reta diretriz está à esquerda do foco:

Colocando a diretriz à direita, temos
Passo 3
Vamos agora ao item (c). Por uma questão de simplicidade, vamos olhar primeiro para o caso em que a diretriz está a direita do foco (Sol). Além disso, como se trata de uma parábola, temos :
Com isso, a órbita é desse tipo:
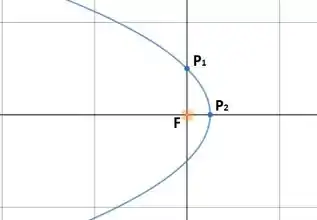
O enunciado disse que era perpendicular a . Com isso já conseguimos achar os pontos e . Em coordenadas cartesianas:
A escala do gráfico é em milhões de quilômetros. A distância mais próxima que o cometa fica do Sol é
Portanto, essa distância é de 5 milhões de quilômetros. No caso em que a reta diretriz está à esquerda do foco, o resultado será o mesmo.
Passo 4
Por fim temos o item (d). Aqui a órbita é elíptica com . Vamos considerar a reta diretriz à direita do foco:
A seguir temos um esboço da situação:

Queremos saber as distâncias dos pontos e para o foco (Sol). O ponto corresponde a , assim :
Já para o ponto , temos com :
Foi dado que o tamanho do semi-eixo maior é 36 milhões de quilômetros, de modo que a distância real entre os pontos e é duas vezes isso: 72 milhoes de quilômetros. Com isso,
Portanto,
Com isso, a menor distância de Mercúrio ao sol é 28,6 milhoes de quilômetros e a maior é 43,4 milhões de quilômetros.