Matrizes e Operações com as Matrizes
Teoria
Introdução às Matrizes
Fala aí! Vamos começar a estudar as matrizes aqui!
Mas pode ficar despreocupado que vamos explorar esse conceito juntos e passo a passo!!
Bom, primeiro a gente tem que conhecer as matrizes. Podemos pensar que a matriz é uma maneira da gente guardar alguns números em linhas e colunas.
Achou estranho? Vamos ver um exemplo aqui. Vamos arrumar os números e dentro de uma matriz que eu vou chamar de (a gente costuma nomear as matrizes com letras maiúsculas). Muito prazer, essa aqui é a nossa primeira matriz:
Simpática, não?
Agora vamos conhecer melhor essa estrutura.
Bem, como eu falei antes, as matrizes possuem uma organização em linhas e colunas
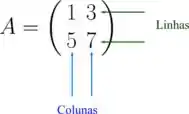
Sabendo a quantidade de linhas e a quantidade de colunas a gente diz o tipo da matriz. Nesse caso a gente fala que essa matriz é uma matriz do tipo ou . Beleza? Dessa forma, uma matriz com linhas e colunas vai ser do tipo .
Uma última coisinha que a gente pode falar sobre as matrizes é que esses números que estão dentro dela são os elementos da matriz e a gente consegue achar eles falando em qual linha e coluna ele está:
O número está na primeira linha e na primeira coluna e a gente fala que ele é o elemento ;
O número está na primeira linha e na segunda coluna e a gente fala que ele é o elemento ;
O número está na segunda linha e na primeira coluna e a gente fala que ele é o elemento ;
O número está na segunda linha e na segunda coluna e a gente fala que ele é o elemento .
Tipos de Matrizes
Vamos começar vendo alguns tipos de matrizes:
Matriz nula: é a matriz em que todos os seus elementos são nulos (ou seja, é uma matriz que possui apenas zeros). É indicada por . Veja um exemplo:
Matriz quadrada de ordem : é uma matriz com o mesmo número de linhas e colunas (). Por exemplo, a seguinte matriz é uma matriz quadrada de ordem 3:
Pois ela tem 3 linhas e 3 colunas.
Diagonal principal: A diagonal principal é formada pelos elementos , ou seja, os elementos em que o índice da linha é igual ao índice da coluna. Por exemplo a matriz a seguir tem todos os elementos da diagonal principal igual a :
Bem, essa foi uma matriz quadrada e a diagonal principal bateu certinho com a diagonal do quadrado mas nem sempre a gente vai ter isso, olha só outras diagonais principais de outras matrizes de tipos diferentes (eu deixei a diagonal principal marcada aqui):
Matriz diagonal: é uma matriz quadrada que só tem elementos diferentes de zero na sua diagonal principal. Os outros são todos iguais a . Olha só:
Matriz identidade de ordem : (denotamos por ou ) é uma quadrada de ordem onde todos os elementos da diagonal principal são iguais a 1 e o restante é zero.
Veja os exemplos:
Matriz triangular superior: é uma matriz quadrada que tenha apenas zeros abaixo de sua diagonal principal.
Por exemplo, toda matriz triangular superior é da seguinte forma:
Não importa se alguma dessas letras for zero também, o que importa é que tem que ter tudo zero abaixo da diagonal principal!!!
Matriz triangular inferior: Ela funciona quase igual à superior, só que ela possui todos os elementos acima da diagonal principal iguais a zero. Por exemplo:
Agora que você já conhece os diferentes tipos de matrizes, vamos ver como que a gente realiza as operações com as matrizes!
Soma e subtração entre matrizes
Vamos começar somando e subtraindo as matrizes. Essas operações vão aparecer dessa forma aqui:
ou
Beleza, mas como que fazemos isso aí?
Antes eu tenho que te falar que a soma e a multiplicação entre matrizes só existe entre matrizes do mesmo tipo. As matrizes tem que ter o mesmo número de linhas e o mesmo número de colunas. Nesse exemplo aí de cima, as duas matrizes têm 3 linhas e 2 colunas, aí a gente consegue fazer essa operação, ok?
Bem, para fazer essas operações a gente tem que tomar prestar atenção nas posições dos elementos das duas matrizes.
Vamos ver a soma primeiro, a gente tem que somar cada elemento de uma matriz com o elemento na mesma posição da outra matriz. Assim ó:
Fazendo essas continhas a gente fica com:
Beleza!! Para a subtração a gente vai fazer a mesma coisa, só que vamos subtrair os elementos de uma matriz com os elementos da mesma posição na outra matriz. Olha só:
Resolvendo essas continhas a gente fica com
Show de bolinhas??
Produtos com matrizes
A gente também pode multiplicar uma matriz por um número. Assim:
A maneira que a gente faz isso é multiplicando todos os elementos da matriz pelo número que a gente está multiplicando. No nosso exemplo a gente vai ter que multiplicar todos os números da nossa matriz por :
Realizandos os produtos a gente tem
Belezinha?
A última operação que a gente pode fazer é multiplicar matrizes. Para fazermos isso, a gente primeiro tem que ver se dá para fazermos a multiplicação. Nem sempre o produto é possível.
Se tivermos duas matrizes e , em que tenha linhas e colunas. A única forma de conseguirmos fazer o produto é se a matriz tenha linhas e quantas colunas ele quiser.
Ficou confuso? O que a gente precisa ter é que o número de colunas de seja igual ao número de linhas de . Por exemplo, eu consigo fazer o produto de uma matriz com uma matriz mas não consigo fazer o produto de uma com uma . Vamos ver um exemplo aqui para ficar mais claro.
Considere as matrizes a seguir:
A gente consegue ver que a matriz tem 2 linhas e 3 colunas enquanto a matriz B tem 3 linhas e 1 coluna. Como a gente viu, eu só consigo fazer o produto de A com B pois o número de linhas de B é igual ao número de colunas de A.
Outra coisa que a gente já consegue ver, é que a gente não conseguiria calcular o produto pois o número de colunas do (1) é diferente do número de linhas de (2). Epa!!! Isso pode? Eu consigo fazer mas não consigo fazer ?! SIIIIIM. Isso é bem comum para as matrizes. Isso quer dizer que esse produto é não comutativo.
Beleza, mas como a gente calcular de fato esses produtos? Vamos lá aprender a fazer isso.
O que você tem que fazer no produto consiste em multiplicar as linhas de A pelas colunas de B. Mas como a gente faz isso? Bem, uma maneira da gente conseguir visualizar isso é escrever as matrizes nessa forma aqui:
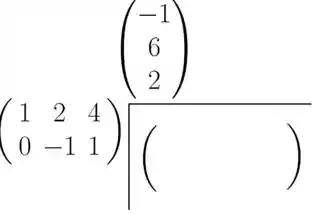
A gente escreve a matriz A (a primeira matriz do produto) embaixo e a matriz B (a segunda matriz do produto) em cima. O resultado do produto vai aparecer naqueles parêntesis vazios ali.
O primeiro elemento do nosso produto vai ser o resultado do produto da primeira linha de A com a primeira coluna de B (que nesse caso só tem uma só). A gente faz esse produto de linha por colunas dessa maneira aqui
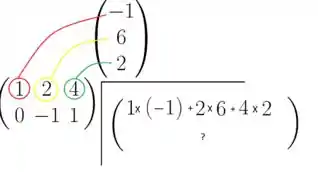
Calculando esses produtos que apareceram, a gente tem
Efetuando a soma, ficamos com:
A gente tem que ir fazendo esses produtos até acabarem as linhas e colunas das nossas matrizes. Resta agora a segunda linha da matriz A. Temos que fazer o produto dessa linha com a primeira coluna. A gente faz igualzinho à primeira linha:
Realizando os produtos, temos
Show! É assim que a gente encontra a resposta do produto entre as matrizes!
Só mais uma última dica. A gente pode saber antes mesmo de fazer o produto entre as matrizes o tipo da matriz que vai ser o resultado.
Como assim?
Bem, olha nosso exemplo, a matriz era do tipo e a do tipo a matriz resposta do produto, que eu vou chamar de C, é do tipo . E daí? A matriz resposta sempre vai ter o número de linhas iguais ao número de linhas da primeira matriz do produto (nesse caso da matriz A) e o mesmo número de colunas da segunda matriz (matriz B nesse caso). Isso vale sempre que o produto é possível!!Olha só, vamos ver algumas matrizes e ver o tipo da matriz que a gente obtem realizando o produto:
- Este produto é impossível!
Isso nos ajuda a saber quantos produtos de linhas e colunas a gente vai ter que fazer e ver se tem alguma coisa errada.
Potências de matrizes
Agora que já conhecemos o produto em matrizes, podemos pensar em potências de matrizes. Mas por quê?
Bom, quando elevamos um número ao quadrado, nós realizamos uma multiplicação desse número por ele mesmo tantas vezes quanto for o número que ele é elevado, por exemplo:
Ou seja, elevado ao número é igual a multiplicar o por ele mesmo vezes.
Podemos aplicar essa mesma idéia para as matrizes, imagine que vamos elevar a seguinte matriz ao cubo:
Logo temos que multiplicar ela por ela mesma vezes:
Vamos começar fazendo o produto das duas primeiras matrizes:
Então nossa matriz elevada ao cubo está assim por enquanto:
Precisamos fazer a última multiplicação:
Após realizar as multiplicações e as somas, chegamos em:
Então chegamos no final da nossa conta:
É isso, isso é tudo que você precisa saber sobre as matrizes e as operações com elas. Agora vamos fazer uns exercícios para ficarmos ainda mais craques nisso??
Tipos de Matrizes
Soma e subtração entre matrizes
Produtos com matrizes
Potências de matrizes
Exercícios Resolvidos
Exercício Resolvido #1
[CCE0002 ÁLGEBRA LINEAR - ESTACIO - 2016.02]
A organização econômica Merco é formada pelos países 1, 2 e 3. O volume anual de negócios realizados entre os três parceiros é representado em uma matriz A, com 3 linhas e 3 colunas, na qual o elemento da linha i e coluna j informa quanto o país i exportou para o país j, em bilhões de dólares. Se A = [ ( 0, 23, 1 ), ( 21, 0, 25), ( 9, 32, 0)] então o país que mais exportou e o que mais importou no Merco foram, respectivamente:
Passo 1
Bom, pessoal, vamos começar a entender de uma vez por todas como funciona essa coisa de matriz!
A matriz nada mais é do que uma estrutura dividida em linhas horizontais:
E colunas verticais:
Passo 2
O enunciado nos diz que os dados sobre exportação e importação de países serão organizados em uma matriz chamada A com as dimensões 3x3, e o que isso quer dizer?
Quer dizer que teremos 3 linhas e 3 colunas, dessa forma:
Nós precisamos organizar os dados que ele nos deu!
Passo 3
Ele nos deu no enunciado a informação: A =[ ( 0, 23, 1 ), ( 21, 0, 25), ( 9, 32, 0)], nada mais é do que os valores das linhas separados pelos parênteses, enquanto o valor das colunas são separados pelas vírgulas. Veja aqui:
A primeira linha será:
(0, 23, 1)
A segunda linha será:
(21, 0, 25)
Enquanto a terceira e última linha será:
(9, 32, 0)
Vamos colocar isso na nossa matriz? Sempre que encontrarmos uma vírgula, vamos passar para a próxima coluna beleza?
Substituindo a primeira linha:
Substituindo a segunda linha:
Substituindo a terceira linha:
Passo 4
Ele nos disse que a coluna informa o país que exportou, enquanto a coluna informa o país que importou. Então a linha 1 corresponde a exportação do país 1, a linha 2 corresponde a exportação do país 2 e a linha 3, a exportação do país 3.
Por outro lado, a coluna diz o quanto cada país importou, a coluna 1 diz quanto o país 1 importou e respectivamente para as outras colunas.
Passo 5
Você concorda comigo que o país que mais exporta é o vendedor do país que mais compra? Vamos ver qual é o maior valor da nossa matriz:
O número 32 corresponde a importação do país 2 e a exportação do país 3, então o país que mais exportou foi o país 3, enquanto o país que mais importou foi o país 2.
Encontramos a resposta!
Fala a verdade, você já está entendendo matrizes, então vamos para mais exercícios!
Resposta
O país que mais exportou foi o país 3, enquanto o país que mais importou foi o país 2.
Exercício Resolvido #2
Elaboração Própria
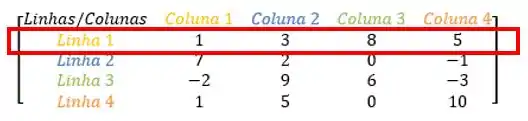
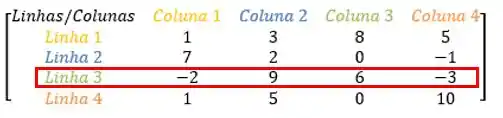
Some os elementos e da matriz:
Passo 1
Vamos aprofundar mais um pouco nosso conhecimento sobre estrutura da matriz:
Já sabemos que ela é dividida entre linhas horizontais e colunas veriticais que são numeradas. Vamos olhar para o nosso caso e numerar nossas linhas e colunas:
Passo 2
Quando falamos que queremos o elemento , estamos dizendo que esse elemento pertence a matriz A:

Olhando nosso exemplo:
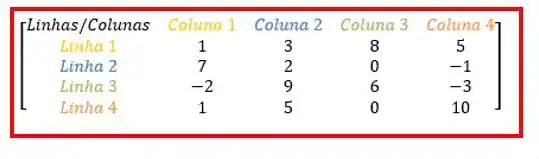
O primeiro número do índice corresponde a linha, nesse caso o elemento pertence a linha :

Olhando nosso exemplo:
O segundo número do índice corresponde a coluna, nesse caso o elemento pertence a coluna :
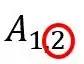
Olhando nosso exemplo:
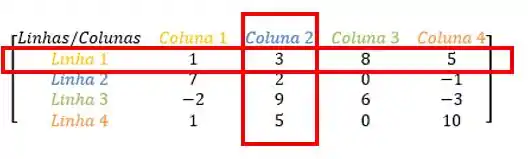
Que elemento é esse? Vamos olhar o que a linha e a coluna têm em comum:
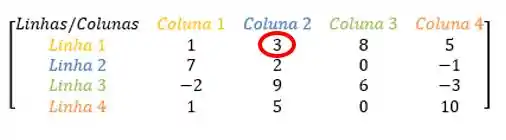
Viu? Achamos o primeiro elemento que queríamos:
Passo 3
Vamos fazer o mesmo para encontrar o segundo elemento que desejamos, :
O primeiro número do índice corresponde a linha, nesse caso o elemento pertence a linha :

Olhando nosso exemplo:
O segundo número do índice corresponde a coluna, nesse caso o elemento pertence a coluna :
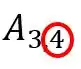
Olhando nosso exemplo:
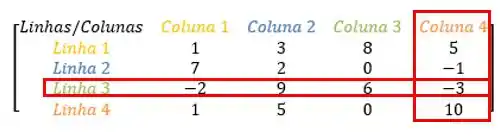
Que elemento é esse? Vamos olhar o que a linha e a coluna têm em comum:
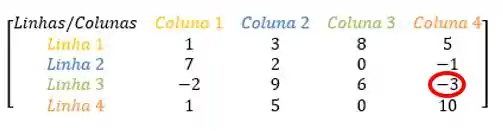
Viu? Achamos o segundo elemento que queríamos:
Passo 4
Calma, ainda não achamos a resposta, porque no enunciado, nos pediram pela soma dos elementos que procuramos, ou seja, a resposta deve ser:
Vamos substituir os valores que encontramos:
E
Logo, a soma será:
Não esquece que o nosso segundo elemento é negativo, ok? Então essa soma se torna:
Chegamos na resposta!
Resposta
A soma é igual a 0.
Exercício Resolvido #3
Elaboração Própria
Dada a matriz A, encontre o valor de 2A:
Passo 1
O primeiro passo aqui é entender o que a questão está pedindo pra gente.
Ao nos dar uma matriz , e pedir que façamos , o que ele quer é que a gente faça a multiplicação da matriz por .
Se:
Então, , será:
Uma multiplicação de uma matriz por um número real!
Passo 2
Mas aí, você me pergunta: Como se faz a multiplicação de uma matriz por um número real?
Simples, vamos multiplicar CADA ELEMENTO DA MATRIZ por esse número real:
Então teremos:
Passo 3
Vamos fazer essas multiplicações?
- 2 1 = 2
- 2 3 =6
- 2 5 = 10
- 2 9 = 18
- 2 8 = 16
- 2 7 = 14
Logo:
Então:
Pronto! Conseguimos chegar na resposta final, meu caro amigo! Repara que cada elemento da nova matriz é exatamente igual ao dobro do elemento correspondente da matriz anterior.
Resposta
Exercício Resolvido #4
[CCE0002 ÁLGEBRA LINEAR - ESTACIO - 2016.02]
Dadas as matrizes A = ( 1 2 3) e B = ( -2 0 1) , podemos afirmar que a matriz 2A + 3B é igual a :
Passo 1
Vamos começar colocando as nossas matrizes naquele formato bonito que gostamos. Então:
Enquanto para a matriz B, temos:
Passo 2
Agora que temos as matrizes e , precisamos encontrar e . Para isso vamos multiplicar as matrizes por número reais!
Mas aíi, você me pergunta: Como se faz a multiplicação de uma matriz por um número real?
Para isso, Simples, caro gafanhoto, vamos multiplicar CADA ELEMENTO DA MATRIZ por esse número real. , Ppor exemplo, a matriz A multiplicada pelo número real :
Então teremos:
Passo 3
Vamos fazer essas multiplicações?
- 2 . 1 = 2
- 2 . 2 =4
- 2 . 3 = 6
- 3 . (-2) = -6
- 3 . 0 = 0
- 3 . 1 = 3
Então chegamos a:
Então:
Chegamos em , agora vamos para !
Passo 34
Se a matriz é:
Então:
Vamos multiplicar cada elemento da matriz por :
Passo 45
Vamos fazer essas multiplicações?
Lembrando que a multiplicação entre números de sinais diferentes tem o resultado com o sinal negativo!
Multiplicação de qualquer número por zero sempre vai ser igual a zero!
Então chegamos a:
Então:
Calma, calma, calma! Ainda não chegamos na resposta, mas não desiste! Vamos somar matrizesJá temos tudo que precisávamos, vem comigo!
Passo 56
O que o enunciado pediu . Então vVamos somar as matrizes e e encontrar uma nova matriz, vamos chamar essa matriz nova de , beleza?
Como já descobrimos que:
E
Então podemos substituir em
Passo 67
Para somar matrizes, devemos garantir que as duas matrizeselas terão o mesmo número de linhas e o mesmo número de colunas. No nosso caso, as duas matrizes e tem o mesmo número de linhas igual a 1, e o mesmo número de colunas igual a 3, entãosendo assim, podemos somar tranquilamente!
E como acontece essa soma? Vamos somar os números que estão na mesma posição, por exemplo, o elemento vai ser somado ao elemento , enquanto o elemento vai ser somado ao elemento !
![]()
Vamos fazer esse exemplo que vou te mostrar:
Então:
Vamos fazer essas somas separadamente então?
Voltando para a matriz
Então chegamos na resposta final:
Resposta
Exercício Resolvido #5
Elaboração própria
Dadas as matrizes A = ( 1 2 3) e B = ( -2 0 1) , podemos afirmar que a matriz A -B é igual a :
Passo 1
Vamos começar colocando as nossas matrizes naquele formato bonito que gostamos. Então:
Enquanto para a matriz B, temos:
Passo 2
Para subtrair matrizes, devemos garantir que as duas matrizes terão o mesmo número de linhas e o mesmo número de colunas. No nosso caso, as matrizes e tem o mesmo número de linhas igual a 1, e o mesmo número de colunas igual a 3, então podemos subtrair tranquilamente!
Passo 3
E como acontece essa subtração? Para isso nós subtraímos os números que estão na mesma posição. Por exemplo, o elemento vai ser subtraído do elemento , enquanto o elemento vai ser subtraído do elemento !
Vamos fazer, que vou te mostrar:
![]()
Os números destacados com a mesma cor estão na mesma posição, então fazemos a subtração entre eles e o resultado dessa operação será mantido também nesta mesma posição formando nosso resultado:
![]()
Passo 4
Vamos fazer essas subtrações separadamente, então?
Subtrair um número negativo é igual a somar esse mesmo número a conta, por isso o 2 era negativo e virou positivo!
Voltando para a matriz, chegamos na resposta final:
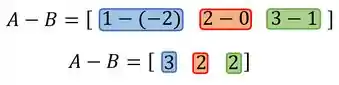
E essa será nossa resposta.
Resposta
Exercício Resolvido #6
[CCE0002 ÁLGEBRA LINEAR - ESTACIO - 2016.02]
Se A é uma matriz 2x3 e B é uma matriz 3x4, então o produto dessas matrizes terá qual dimensão?
Passo 1
Bom, na multiplicação de matrizes, precisamos sempre prestar atenção em um critério: o número de colunas da primeira matriz deve ser igual ao número de linhas da segunda. Ou seja, se temos:
Sendo uma matriz com colunas, a matriz tem que ter linhas para que a multiplicação seja possível.
Passo 2
Mas qual é o motivo pra isso? Vamos fazer um exemplo de multiplicação de matrizes pra isso ficar bem claro. Imagina uma matriz A:
é uma matriz 1x2, ou seja, a matriz te 1 linha e 2 colunas. Por outro lado, temos a matriz
Enquanto a matriz é uma matriz 2x3, pois tem 2 linhas e 3 colunas.
A multiplicação entre elas é possível:
Pois, temos o número de colunas da matriz é igual ao número de linhas da matriz :

E podemos prever que a matriz resultante dessa multiplicação, terá o mesmo número de linhas que a primeira matriz e o mesmo número de colunas da segunda matriz, nesse caso, a matriz resultante da multiplicação entre e , terá 1 linha ( tem 1 linha) e colunas ( tem 3 colunas).
Passo 3
O resultado da multiplicação de matrizes será uma nova matriz que tem seus elementos formados pela seguinte regra:
Para encontrar o valor de , faremos a soma dos produtos entre os elementos da primeira linha da matriz com a primeira coluna da matriz , veja:
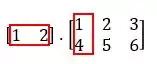
Logo:
Agora vamos encontrar o elemento . Para isso faremos a soma dos produtos entre os elementos da primeira linha da matriz com a segunda coluna da matriz , veja:
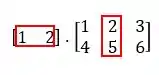
Logo:
E por último, para encontrar , faremos a soma dos produtos entre os elementos da primeira linha da matriz com a terceira coluna da matriz , veja:
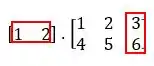
Logo:
Formando assim a matriz resultante.
Passo 4
Vimos com o nosso exemplo, que o que determina as dimensões da matriz resultante da multiplicação entre duas outras matrizes é o número de linhas da primeira matriz e o número de colunas da segunda:
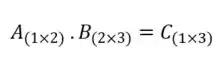
Entendeu direitinho? Agora vamos voltar para o enunciado!
Passo 5
No enunciado, falamos que temos a matriz de dimensões 2X3, enquanto a matriz tem as dimensões 3X4, logo temos:
Então essas matrizes podem ser multiplicadas e as dimensões da matriz resultante serão:
Resposta
Exercício Resolvido #7
[CCE0002 ÁLGEBRA LINEAR - ESTACIO - 2016.02]
As matrizes e são tais que a operação A x (B + C) é possível. Nessas condições, determine quais as dimensões da matriz resultante.
Passo 1
Vamos com calma e firmeza no que já sabemos sobre matrizes!
Primeiro de tudo: em qualquer expressão matemática, sempre começamos a resolver pelo que está dentro dos parênteses. Ou seja:
Para que seja possível somar as matrizes e , elas precisam ter as mesmas dimensões, e a matriz resultante também deve manter essas mesmas dimensões. Como, as dimensões de são (m x n), e as dimensões de são (m x 4). Então:
Não sabemos quem é o número de linhas (), mas como o enunciado disse que as operações são possíveis, então as duas matrizes só podem ter o mesmo número de colunas.
Logo:
E encontramos uma pista para a nossa solução.
Foi? Ótimo! Vamos dizer que essa soma seja igual a uma matriz resultante :
Passo 2
Qual é a dimensão de ? Como ela é o resultado da soma de e . As dimensões de serão as mesmas de e . Ou seja:
Passo 3
Agora vamos olhar a multiplicação entre e o resultado da soma anterior:
Bom, como o enunciado mesmo disse, esse resultado é possível, mas sabemos que para realizar uma multiplicação entre matrizes, precisamos que o número de colunas da primeira matriz seja igual ao número de linhas da segunda matriz:

Então encontramos outra pista. Ou seja:
Passo 4
Temos a multiplicação entre matrizes:
Portanto, o resultado será uma matriz com o mesmo número de linhas da matriz e o mesmo número de colunas da matriz :
E chegamos no resultado final!
Resposta
A dimensão da matriz resultante será igual a:
Exercício Resolvido #8
[CCE0002 ÁLGEBRA LINEAR - ESTACIO - 2016.02]
Calcule o sendo e
Passo 1
Para que seja possível realizar uma multiplicação entre matrizes, temos que ter o número de colunas da primeira matriz igual ao número de linhas da segunda matriz, ou seja:
Nesse caso, podemos ver que a matriz tem 2 linhas e 1 coluna, enquanto a matriz B tem 1 coluna e 2 linhas. Logo o resultado da multiplicação entre essas duas matrizes será uma nova matriz de dimensões .
Passo 2
Então, vamos multiplicar essas matrizes:
Olhando elemento por elemento, vemos que:
O está na primeira linha e na primeira coluna da matriz resultante. Então, para encontrar o valor de , precisamos multiplicar a primeira linha de com a primeira coluna de :

Logo:
Já o está na primeira linha, mas na segunda coluna. Então, para encontrar o valor de ,precisamos multiplicar a primeira linha de com a segunda coluna de :
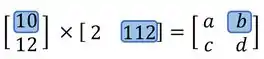
Logo:
Agora vamos olhar para o , que está na segunda linha e primeira coluna da matriz resultante. Assim, para encontrar o valor de ,precisamos multiplicar a segunda linha de com a primeira coluna de :

Logo:
Por fim, vemos que o está na segunda linha e na segunda coluna da matriz resultante. Logo, para encontrar o valor de ,precisamos multiplicar a segunda linha de com a segunda coluna de :
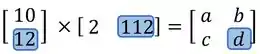
Logo:
Perceba que é a posição de cada elemento quem determina quais as linhas e colunas que serão multiplicadas.
Com isso chegamos então na resposta final! E encontramos nossa resposta.
Resposta
Exercício Resolvido #9
Elaboração própria
Passe o sistema linear:
Para a forma matricial.
Passo 1
Bom pessoal, vamos pra mais um exercício. Você está vendo esse conjunto com as equações? São três equações:
Cada uma das equações tem três incógnitas , mas não estamos interessadas nas incógnitas, e sim, nos coeficientes que as acompanham, por isso vamos colocar todos os coeficientes junto das incógnitas. Lembrando que quando ela estiver sozinha, significa que seu coeficiente é igual a 1.
Então:
Passo 2
Nossa matriz será montada olhando a organização das equações:
São equações, então teremos linhas. E são incógnitas, mais um termo independente que está do lado direito do sinal de =. Então termos colunas.
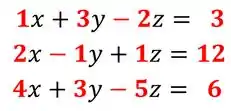
São os valores dos coeficientes de cada incógnita que vamos colocar na nossa matriz. E vamos organizá-los na ordem que vieram, ou seja, os valores dos coeficientes da primeira equação serão colocados na primeira linha, os da segunda equação na segunda linha e assim por diante.
Outro detalhe importante é que cada coluna vai corresponder aos coeficientes de uma determinada incógnita. Sendo assim, na primeira coluna, temos os coeficientes de , na segunda de , na terceira de , e na quarta estão os valores que ficaram do lado direito das igualdades.
Perceba uma coisa, o sinal de positivo e negativo de cada coeficiente é considerado na matriz.
Pronto, observado a organização das equações, chegamos na resposta final!
Resposta
Exercício Resolvido #10
Elaboração própria
Dado que a matriz é dada pelos coeficientes numéricos do seguinte sistema linear:
E que seja igual a 2A. Defina os elementos que faltam da matriz
Passo 1
Vamos começar colocando o sistema linear na sua forma matricial, ok? O sistema é:
Vamos destacar quem devemos colocar na matriz:
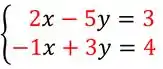
Lembrando que vamos colocar os coeficientes da primeira equação na primeira linha da matriz e os coeficientes da segunda equação na segunda linha:
Passo 2
Agora que já sabemos quem é a matriz , vamos multiplicar ela por 2 para descobrir quem é a matriz :
Beleza, nesse caso de multiplicação de uma matriz por um número real, devemos multiplicar todos os elementos dessa matriz pelo mesmo 2, dessa forma:
Vamos fazer essas multiplicações separadamente, ok?
Passo 3
Colocando os resultados em seus lugares:
Conseguimos então chegar aos resultados que faltam:
Ótimo, pessoal!
Resposta
Os resultados restantes são: -2, 6 e 6
Exercício Resolvido #11
Elaboração Própria
Considere as matrizes e resolva:
Passo 1
Vamos láá!! Temos duas matrizes e queremos fazer as operações indicadas com elas. Então vamos começar!

a) Para fazermos a diferença vamos substituir as matrizes
Assim,
Portanto,
Beleza?!
Passo 2
Já na letra (b) temos o contrário,
Substituindo as matrizes,
Assim,
Portanto,
Show de bola?!
Passo 3
c) Aqui iremos fazer a soma das duas matrizes,
Substituindo as matrizes, temos
Assim,
Portanto,
Passo 4
Agora vamos realizar as duas multiplicações!!

d) A primeira multiplicação é
Fazendo a multiplicação, teremos
Fazendo as contas,
Assim,
e) Pra finalizar, faremos
Fazendo a multiplicação, teremos
Fazendo as contas,
Assim,
Show de bola?!