Sistemas Lineares
Teoria
Fala aíííííí! Vamos começar os nossos estudos de sistemas lineares... é, você não leu errado, vamos estudar sistemas lineares mesmo!
Vamos lembrar o que é um sistema linear? É um conjunto de equações que envolvem uma ou mais variáveis a serem descobertas. Ele tem essa carinha aqui
Em que a gente quer encontrar o e o que satisfazem esse sistema linear. Existem algumas técnicas que a gente aprende na escola para resolver esses sistemas mas aqui a gente vai aprender como resolver isso usando matrizes. E o legal é que o procedimento que eu vou te ensinar serve para quaisquer sistemas lineares!
Se você está estranhando que não apareceu nenhuma matriz aqui, pode ficar aliviado. A matriz está escondidinha ali, vamos entender isso agora.
Matriz ampliada e matriz dos coeficientes
Bom, para transformarmos um sistema linear em uma matriz, vamos primeiro prestar atenção nos números que a gente tem no nosso sistema linear:
Os números que eu marquei de vermelho são os coeficientes do nosso sistema linear e os números em azul são os resultados mesmo. Se a gente pegar o sistema do jeito que está a gente já consegue montar a nossa matriz.
Vamos montar ela aos poucos. A estrutura da nossa matriz vai ser a seguinte:
- O número de linhas da matriz vai ser o número de equações que o sistema linear possui;
- O número de colunas da matriz vai ser o número de incógnitas + 1 (a gente soma esse 1 aí pois uma das colunas vai estar responsável pelos resultados do nosso sistema linear).
Como no nosso sistema linear nós temos 2 equações e 2 incógnitas, nossa matriz vai ter 2 linhas (associadas ao número de equações) e 3 colunas (associadas ao número de incógnitas + 1):
Nossa tarefa agora é preencher esses espaços da nossa matriz. Vamos fazer isso conhecendo coluna a coluna.
A primeira coluna da nossa matriz vai estar associada à incógnita . Ela deve carregar todos os coeficientes de que aparecem no nosso sistema linear. Dando uma olhada nele, nós temos que na primeira equação o está sendo multiplicado por e na segunda por . Muito bem, agora é só colocar esses números na nossa matriz seguindo a ordem que aparecem no nosso sistema linear
Já a segunda coluna da nossa matriz vai estar associada à incógnita . Ela deve carregar todos os coeficientes de que aparecem no nosso sistema linear. Dando uma olhada nele, nós temos que na primeira equação o está sendo multiplicado por e na segunda por . Muito bem, agora é só colocar esses números na nossa matriz seguindo a ordem que aparecem no nosso sistema linear
Belezaa! Só falta preencher a última coluna. Nessa última coluna, só nos resta por os resultados do nosso sistema linear na ordem que eles aparecem. Então a nossa matriz fica assim:
Prontinho! Conseguimos escrever o nosso sistema como uma matriz. Essa matriz aí é a chamada matriz ampliada do sistema e também é comum que ela apareça dessa forma aqui:
Antes de começarmos a resolver esse sistema, vale dizer que podemos construir uma matriz com apenas os coeficientes do nosso sistema linear:
Essa é a conhecida matriz dos coeficientes. Beleza! Vamos agora ver como resolvemos isso aí.
Resolvendo sistemas lineares
Para resolver esse sistema linear usando as matrizes a gente vai precisar transformar a matriz ampliada em sua forma escalonada. Eu vou fazer todo o procedimento com vocês aqui e pode ficar tranquilo que ele vale sempre, ok? Vamos lá então. Nossa matriz é essa daqui:
Beleza, vamos lembrar como que a gente escalona uma matriz. A gente olha o primeiro elemento da primeira linha e temos que zerar todos os elementos abaixo dele. Feito isso, a gente vai pro segundo elemento da segunda linha e zera os elementos abaixo dele.... e por aí vai, até a última linha.
Vamos começar.
O primeiro elemento da primeira linha é o número . Abaixo dele a gente tem o número que a gente precisa zerar. A gente consegue zerar esse 2 da segunda linha fazendo a seguinte operação elementar:
Realizando esta operação na nossa matriz, ficamos com
Fazendo esses produtos temos
Chegamos à sua forma escalonada!
Tá, mas e daí? Bem, essa forma escalonada já ajuda demaaais a nossa vida. Quando chegamos nesse ponto a gente volta para a forma do sistema linear.
Lembra que eu falei que na primeira coluna estão os números que vão estar multiplicando a incógnita números que vão estar multiplicando a incógnita , na segunda coluna vão estar os coeficientes da incógnita e na terceira os resultado? Então, a gente vai usar essas informações para resgatar a cara de um sistema linear. Olha só como fica:
Agora a gente pode realizar os produtos que apareceram e escrever nosso sistema linear com uma carinha mais bonitinha:
Pois . Já viu a vantagem? Não?Não tem problema, olha só a segunda equação:
Ela já nos dá o valor de . Vamos passar esse da direita para a esquerda. Como ele estava multiplicando, quando ele passa para o outro lado, ele passa dividindo:
Opaa. Já achamos uma incógnita! Que maravilha!Agora, a gente usa esse valor que encontramos na primeira equação
Passando esse 3 para o outro lado da igualdade e trocando seu sinal, ficamos com
E assim a a gente resolveu o sistema linear. Sempre que se deparar com um sistema linear segue esse roteiro:
- Escreva a matriz ampliada desse sistema linear;
- Escalone essa matriz;
- Depois de obter a matriz escalonada, volte com os coeficiente, volte com o sistema linear;
- A última linha do seu sistema linear já vai te fornecer uma das incógnitas do sistema;
- Use o valor da incógnita, que você obteve, na linha acima daquela que você usou antes e encontre outra incógnita;
- Repita esse procedimento até encontrar todas as incógnitas do sistema.
Classificação de um sistema linear
Já vimos como se resolve um sistema linear. Agora, vamos aprender como a gente classifica um sistema linear.
Algumas vezes vai ser interessante classificarmos o sistema linear para ver se a gente vai ou não conseguir encontrar alguma resposta nele. Como assim? Bem, existem sistemas lineares que são como os que a gente fez aqui em cima, possuem uma única solução para cada uma das incógnitas. Quando isso acontece, dizemos que o sistema linear é possível e determinado.
Maaaas, existem sistemas lineares em que podemos encontrar várias respostas para cada uma das variáveis. Quando isso acontece, dizemos que o sistema é possível e indeterminado.
Por fim, existem sistemas lineares em que a gente não consegue achar resposta alguma para as incógnitas. Estes são os sistemas impossíveis.
Aqui a gente vai ver um procedimento para classificarmos o tipo do sistema linear sem precisar resolvê-lo. Vamos lá!
Vamos considerar o sistema linear a seguir
Vamos precisar escrever a matriz ampliada do nosso sistema. Como temos 3 equações e 3 incógnitas , nossa matriz ampliada vai ter 3 linhas e 4 colunas. Como vimos aqui, nosso sistema linear se torna:
O próximo passo é escalonar a matriz ampliada. Vamos lá.
Precisamos, primeiro, zerar os elementos abaixo do primeiro elemento da primeira linha que é o número 1. A maneira que eu vou fazer para zerar aquele 2 e 1 ali vai ser realizando as operações elementares abaixo:
Fazendo isso na nossa matriz ficamos com:
Lembrando que com dá e realizando os produtos temos
Beleza, nossa primeira linha já está ok no nosso processo de escalonamento. Vamos para a segunda linha. Precisamos zerar os números abaixo daquele da segunda linha. Então precisamos zerar aquele da terceira linha. Maravilha, a gente faz isso através dessa operação aqui
Isso nos leva a
Lembrando que com dá temos
Opa, que isso, acabou zerando a linha 3 todinha. Devo me preocupar? Não, isso encerra nosso escalonamente também.
Beleza, com a matriz ampliada escalonada a gente já pode classificar nosso sistema linear. Antes, deixa eu separar quem é a matriz ampliada escalonada e quem é a matriz dos coeficientes pois a nossa análise vai ser em cima dessas duas matrizes.
Matriz ampliada:
Matriz dos Coeficientes:
Com essas duas matrizes em mão só falta eu definir um carinha importante, o posto de uma matriz. O posto de uma matriz é o número de linhas não nulas dessa matriz. Então, o posto da matriz ampliada é pois a matriz ampliada possui duas linhas não nulas. O posto da matriz dos coeficientes é pois a matriz dos coeficientes possui duas linhas não nulas.
Outra coisa que vai ser última vai ser chamar o número de linhas da nossa matriz ampliada de , nesse exemplo temos que .
Agora sim, temos tudo que a gente precisa para classificar um sistema linear. É bem direto, são 3 regrinhas que definem o sistema. São elas:
- Se o posto da matriz ampliada for igual ao número de linhas da matriz ampliada , o sistema é possível e determinado (SPD);
- Se o posto da matriz ampliada for menor que o número de linhas da matriz ampliada , o sistema é possível e indeterminado (SPI);
- Se o posto da matriz ampliada for diferente do posto da matriz dos coeficientes , o sistema é impossível.
No nosso caso, como na matriz ampliada temos e ficamos com o seguinto caso, o caso em que . Então, nosso sistema linear é possível e indeterminado ou a gente usa a sigla SPI para fazer um charme.
Bom galera, é isso, aprendemos tudo sobre resolver um sistema linear usando as matrizes.
Agora, para ficarmos fera, vamos fazer uns exercícios?
Te vejo lá 😊
Resolvendo sistemas lineares
Classificação de um sistema linear
Exercícios Resolvidos
Exercício Resolvido #1
Apostila Sistemas Lineares
Consideremos o seguinte sistema de equações lineares dadas como matriz, ache as soluções:
Passo 1
Faaaala galerinhaa !! Prontos para mais uma ?!
Que estranho... o exercício dá uma matriz e nos pede para resolver um sistema linear... Cadê o sistema linear?!
Calma!
Essa matriz que tá aparecendo é chamada de matriz ampliada do sistema linear. Cada linha representa uma equação do sistema, e a gente pode pensar nas colunas assim: A primeira coluna contém os números que vão multiplicar o , na segunda coluna a gente tem os números que vão multiplicar o e na última coluna, a gente tem os resultados:
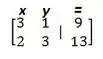
Essa matriz é a mesma coisa que esse sistema aqui ó:
Boom galerinha, o escalonamento é algo bem importante, não é?
Isso porque nós podemos escrever sistemas lineares na forma de uma matriz, e ao escalonar nós conseguimos achar a solução do problema de forma mais fácil do que substituindo um no outro, como fazíamos lá no ensino médio !!
Vamos começar achando o pivô para a primeria coluna, certo?
E como faremos para fazer aparecer o 1 no lugar do 3?
Podemos fazer:
Então:
Agora nós vamos precisar zerar estes termos abaixo do pivô, ok? Isso vai facilitar na hora de resolvermos nosso sisteminha!
Para isso podemos fazer:
Então:
Para resolver essa operação com frações na segunda linha a gente faz:
Então nossa matriz fica dessa forma aqui:
Bom, nós podíamos seguir a achar o pivô para a segunda coluna, mas quando chegamos nesse ponto nós já achamos uma incógnita em função do resultado, certo?
Como assim?
Bom, a segunda linha representa a segunda equação, a primeira coluna o x, a segunda o y e a terceira a igualdade !! Se é assim, na segunda linha nós temos o x nulo, então o y está em função da igualdade!!
Passo 2
Podemos transformar esta matriz novamente em sistemas lineares
Na segunda equação nós podemos isolar o y, certo?
Vamos passar quem tá multiplicando o para o outro lado da igualdade. Cuidado que quando a gente faz isso, quem multiplica passa a dividir e quem dividi passa a multiplicar:
Na primeira equação nós podemos substituir o y pelo que acabamos de achar:
Agora o 1 vai lá para o outro lado da igualdade com o sinal oposto:
Olha que massa !!
Acabamos de achar a solução:
Bora continuar ?!
Resposta
Exercício Resolvido #2
Apostila Sistemas Lineares
Consideremos o seguinte sistema de equações lineares dadas como matriz, ache as soluções:
Passo 1
Mais uma beem legal !! Animados para seguir?
Já vimos que cada linha representa uma equação, e cada coluna um companheiro para as letrinhas assim como o resultado:
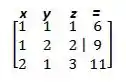
A primeira linha já veio com o pivô para facilitar a nossa vida, certo?
Então vamos começar pensando em como zerar os números abaixo dele, 1 e 2, ok?
Para isso nós podemos fazer as seguintes operações:
Então:
E com isso nós já achamos o pivô para a segunda coluna, certo?
Então vamos tentar zerar esse -1 que está em baixo dele, certinho?
Vamos fazer isso somando a linha 3 com a 2, assim dá certo, concordam?
Então:
Nós podíamos manipular mais, mas só até esse ponto já nos facilita, e muito, a vida, não é?
Passo 2
Se nesse ponto ela já nos ajuda, então só nos resta transformá-la em equações lineares !!
Lembrando que cada linha é uma equação linear, a primeira coluna é o par do x, a segunda do y, a terceira do z e última a igualdade:
Da terceira linha nós conseguimos achar o z:
O 2 que está do ladinho de z passa para o outro lado dividindo, certo?
Na segunda coluna nós podemos achar o y, basta substituirmos o z:
O 1 vai passa para o outro lado da igualdade com o sinal oposto, e deixar o y sozinho, só assim pra gente conseguir achá-lo:
Na primeira equações nós podemos substituir o y pelo que acabamos de achar:
E agora é a vez do 3 passar com sinal oposto para o outro lado:
E assim nós achamos a solução para este sistemaa !!
Gostaram?!
Resposta
Exercício Resolvido #3
Apostila Sistemas Linaeares
Consideremos o seguinte sistema de equações lineares dadas como matriz, ache as soluções:
Passo 1
Shoow de boola !!!
Nada muito diferente da anterior, mas essa matriz representa equações lineares !!
Cada linha representa uma equação, e cada coluna um companheiro para as letrinhas assim como o resultado:

A terceira linha é toda nula, ou seja, não temos pivô para a variável z, e o que isso nos diz?
Nos diz que z é uma variável livre, ou seja, pertence aos números reais e pode ter qualquer valor, então nós vamos colocar as outras variáveis em função dela !!
Bom, a nossa matriz já tem os pivôs, então só nos resta transformá-la novamente em equações lineares !!
Lembrando que cada linha é uma equação (2) e a primeira coluna representa o par do x, a segunda de y, a terceira de z e a ultima a igualdade:
Na segunda equação nós podemos isolar o y passando o termo 2z para o outro lado da igualdade com sinal contrário:
Apesar de ser feio o que achamos, é isso mesmo que é o valor de . Como temos infinitos valores possíveis de , nosso y e x vão ficar escritos em função do z mesmo, não se assustem.
Na primeira equação nós podemos substituir o y pelo que acabamos de achar:
O 2 multiplica cada um dos termos que estão dentro dos parêntesis:
Passando o 18 e z para o outro lado da igualdade com sinal oposto:
Olha que massa !!
Acabamos de achar a solução:
Então, para cada valor de z diferente, teremos valores diferentes para o x e y também !!
Esse tipo de resposta é bem comum e a gente diz que o sistema linear é possível e indeterminado.
Bora continuar ?!
Resposta
Exercício Resolvido #4
Apostila Álgebra Linear
Consideremos o seguinte sistema de equações lineares, ache as soluções:
Passo 1
Boom galerinha, o escalonamento é algo bem importante, não é?
Isso porque nós podemos escrever sistemas lineares na forma de uma matriz, e ao escalonar nós conseguimos achar a solução do problema de forma mais fácil do que substituindo um no outro, como fazíamos lá no ensino médio !!
Então vamos montar uma matriz onde cada linha corresponde a uma equação linear e cada coluna representa o companheiro do assim como o resultado!!
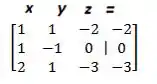
Só colocamos as equações como matriz certo?
A primeira coluna já tem o seu pivô!! Então vamos zerar a segunda e a terceira linha, certo?
Para fazer isso nós podemos usar a primeira linha e manipular a segunda e terceira juntinho! Vamos pensar aqui em uma operação:
Agora vamos só fazer as continhas:
Para encontrar o pivô da segunda nós precisamos transformar este 2 aí em 1, por isso nós podemos dividir toda essa segunda linha por dois, ok?
Então:
E para zerar o termo abaixo desse pivô? O que faremos?
Podemos subtrair a linha 3 de 2, certo?
Então:
Passo 2
A terceira linha é toda nula, ou seja, não temos pivô para a variável z, e o que isso nos diz?
Nos diz que z é uma variável livre, ou seja, pertence aos números reais e pode ter qualquer valor, então nós vamos colocar as outras variáveis em função dela !!
Bom, a nossa matriz já tem os pivôs, então só nos resta transformá-la novamente em equações lineares !!
Da primeira linha:
Na segunda coluna nós podemos isolar o y passando o termo z para o outro lado da igualdade com sinal contrário:
Na primeira equação nós podemos substituir o y pelo que acabamos de achar:
Somando os termos contendo o z:
Os termos 1 e z passam para o outro lado da igualdade com o sinal oposto:
E assim nós acabamos de achar a solução:
Então, para cada valor de z diferente, teremos um ponto diferente !!
O que acharam desta?
Resposta
Exercício Resolvido #5
Apostila Estácio
Ache a solução para o seguintes sistemas lineares:
Passo 1
Vamos seguindo??
Nós vamos montar uma matriz onde cada linha corresponde a uma equação linear e cada coluna representa o companheiro do assim como o resultado!!
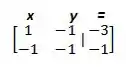
A primeira coluna já tem o seu pivô!
Então vamos zerar o número -1 logo abaixo, e para isso podemos fazer:
Então:
Agora precisamos achar o pivô para a segunda, certo?
E como faremos?
Se dividirmos a linha 2 por -2 dá certinho, não dá? Então boora:
Sendo assim:
Transformando novamente em equações lineares:
Substituindo o y na primeira equação:
Passamos o 2 pra o outro lado igualdade com o sinal oposto:
Olha só !!
Acabamos de achar a nossa solução:
Shoow de bolinhas ?
Resposta
Exercício Resolvido #6
Apostila Álgebra Linear
Consideremos o seguinte sistema de equações lineares, ache as soluções:
Passo 1
Animados para mais uma solução bem legal ?! Entãao boora !!
Nós vamos montar uma matriz onde cada linha corresponde a uma equação linear e cada coluna representa o companheiro do assim como o resultado!!
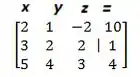
Só colocamos as equações como matriz certo?
Para achar o pivô na primeira coluna podemos dividir tudo por 2, certo?
Então:
Agora precisamos zerar estes números abaixo do nosso pivô na primeira coluna, e aí ? Como faremos?
Que tal usarmos:
Então:
Agora, temos que achar o pivô para a segunda coluna, e para isso podemos transformar em 1 multiplicando tudo da linha 2 por -2:
Então:
Para zerar o termo na última linha podemos fazer:
Então:
Quando chegamos nesse ponto nós já facilitamos muito as coisas, certo?
Passo 2
Agora vamos transformá-la novamente em equações lineares !!
Não se esqueçam que cada linha correspondem a uma equação, cada coluna representa um companheiro para o x, y, z e a igualdade:
Da terceira equação nós podemos achar o z, basta passar o 7 para o outro lado dividindo:
Na segunda equação nós substituímos o z:
Passando o termo 30 para o outro lado da igualdade com sinal contrário:
Na primeira equação nós podemos substituir o y e o z:
O termo 4 passa para o outro lado da igualdade com o sinal oposto:
E assim nós finalizamos mais umaa !!
Legal, não é?
Resposta
Exercício Resolvido #7
Apostila PUC
Ache as soluções para a matriz:
Passo 1
Faaaaaala meus queridos !! Como vocês estão?
Animadíssimos para seguir, eu espero!!
Nós vamos montar uma matriz onde cada linha corresponde a uma equação linear e cada coluna representa o companheiro do assim como o resultado!!

A primeira coluna já tem o seu pivô!
Então vamos zerar o número 2 logo abaixo, para isso podemos fazer:
Então:
A segunda coluna só tem zero, então nós não podemos transformá-la em pivô !
Mas a terceira já tem um -1 ali na posição !! Então vamos simplesmente multiplicar a linha toda por -1:
Então:
Na coluna do y nós não temos o pivô, o que isso significa?
Que y é uma variável livre, ou seja, pertence aos números reais e pode ter qualquer valor, então nós vamos colocar as outras variáveis em função dela !!
Vamos fazer mais uma manipulação para facilitar, zerando o 2 lá na primeira linha:
Então:
Quando chegamos nesse ponto nós já facilitamos muito as coisas, certo?
Passo 2
Agora vamos transformá-la em equações lineares !!
E o y nós já sabemos que é livre !!
E assim nós acabamos de achar a solução:
Legal, não é?
Resposta
Exercício Resolvido #8
Apostila UFTPR
Resolva o sistema:
Passo 1
Mais uma de escalonamento e sistemas lineares para vocês ficarem craques !!
Primeiro vamos transformar as equção em linhas de uma matriz, certo?
Cada linha corresponde a uma equação linear e cada coluna representa o companheiro do assim como o resultado!!
A primeira linha já tem pivô, então vamos zerar o 2 e o 3 abaixo dele:
Então:
Para chegar ao pivô na segunda linha vamos dividir a linha 2 por 3, certo?
Então:
Agora o que nós precisamos fazer? Zerar o 2 abaixo do pivô, e para isso podemos fazer:
Então:
Quando chegamos nesse ponto nós já facilitamos muito as coisas, certo?
Passo 2
Agora vamos transformá-la em equações lineares !!
A segunda equação já nos dá o valor de y, certo? E a terceira está quase pronta, basta nós passarmos o -2 para o outro lado dividindo:
Agora nós vamos colocar o y e z na primeira equação:
Como o denominador é o mesmo para as duas frações podemos somar os numeradores:
Passando o 1 para o outro lado com o sinal oposto:
Acabamos de achar a solução:
E assim nós chegamos ao fim de mais umaaa !!
Resposta
Exercício Resolvido #9
Apostila Álgebra Linear
O sistema linear:
Admite a solução . Determine a soma
Passo 1
Animados para mais uma solução bem legal ?! Entãao boora !!
Nós vamos montar uma matriz onde cada linha corresponde a uma equação linear e cada coluna representa o companheiro do assim como o resultado!!
Para chegar ao pivô na primeira linha basta nós multiplicarmos ela por -1, certo?
Então:
Agora o que nós precisamos fazer? Zerar os dois números abaixo do pivô, e para isso podemos fazer:
Então:
Para achar o pivô da segunda coluna vamos dividir tudo por 2?
Então:
E para zerar o termo -2 abaixo do pivô:
E agora a matriz vai ficar assim:
Quando chegamos nesse ponto nós já facilitamos muito as coisas, certo?
Passo 2
Agora vamos transformá-la em equações lineares !!
Para isolar o z nós vamos usar a terceira equação, para isso nós vamos passar o -2 para o outro lado dividindo:
Agora nós vamos colocar o z na segunda equação:
Agora o 1 passa para o outro lado com o sinal oposto:
E para achar o x nós colocamos y e z na primeira equação:
O termo 6 passa para o outro lado da igualdade com o sinal oposto:
Acabamos de achar a solução:
Mas o que queremos de verdade é , então se já sabemos todos os valores nós vamos só somar !
Legal, não é?
Resposta
Exercício Resolvido #10
Apostila Estácio
Uma loja de discos classificou seus CDS em três tipos A, B e C, unificando o preço para cada tipo. Quatro consumidores fizeram compras nessa loja nas seguintes condições: o primeiro comprou 2 CDs do tipo A, 3 do tipo B e 1 do tipo C, gastando R$121,00. O segundo comprou 4 Cds do tipo A, 2 do tipo B e gastou R$112,00. O terceiro comprou 3 CDs do tipo A, 1 do tipo C e gastous R$79,00. O quarto comprou um CD de cada tipo. Calcule quanto o quarto consumidor pagou à loja.
Passo 1
Faaaaaala sério galerinha !! Essa é legal demais !
O problema quer saber quanto o quarto consumidor pagou à loja, se ele comprou 1A, 1B e 1C. Vamos ter que colocar isso aí em forma de soma, não é?
Para saber a resposta nós vamos precisar achar o valor de cada um deles, e como faremos isso??
Montando um sistema de equações lineares !!
Para o primeiro: comprou 2A, 3B e 1C e pagou 121, então:
Para o segundo: comprou 4A e 2B e pagou 112, então:
Para o terceiro: comprou 3A e 1C e pagou 79, então:
Então o nosso sistema linear será composto destas três equações:
Passo 2
Com as equações nós vamos montar uma matriz onde cada linha corresponde a uma equação linear e cada coluna representa o companheiro do assim como o resultado!!
Para chegar ao pivô na primeira linha basta nós dividirmos ela por 2, certo?
Então:
Agora o que nós precisamos fazer? Zerar os dois números abaixo do pivô, e para isso podemos fazer:
Então:
Para achar o pivô da segunda coluna vamos multiplicar tudo por -1/4?
Então:
E para zerar o termo -4,5 abaixo do pivô:
E agora a matriz vai ficar assim:
Quando chegamos nesse ponto nós já facilitamos muito as coisas, certo?
Passo 3
Agora vamos transformá-la em equações lineares, de noovo !!
Para isolar o C nós vamos usar a terceira equação, passando o 1,75 para o outro lado dividindo:
Agora nós vamos colocar o C na segunda equação:
Agora o 12,5 passa para o outro lado com o sinal oposto:
E para achar o A nós colocamos B e C na primeira equação:
O termo 42,5 passa para o outro lado da igualdade com o sinal oposto:
Acabamos de achar a solução:
Mas nós não queremos saber isso !! Nós queremos saber quanto foi que o quarto comprador pagou, olhando no Passo 1:
Substituindo:
Legal, não é?