Cilindros
Teoria
Definição, Equação e Conceitos
Fala, galerinha do bem! Neste tópico, vamos bater um papo sobre cilindros! Mas antes, vamos lembrar da equação da circunferência? Afinal, a base de um cilindro é um círculo né!
Então, quando eu tenho um círculo de raio , por exemplo, eu tenho essa equação,
E o gráfico fica assim,
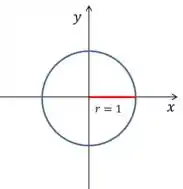
Agora se eu quiser transformar esse gráfico em um gráfico em , com compentes em , tranformando-o em um cílindro. Como ficaria a minha equação? Como seria o gráfico?
Então, galerinha, quando tiver fazendo essa transformação, eu estarei “empilhando” as circunferências no meu eixo . Com isso, eu posso manter minha equação no plano e dizer que ela se matém ao longo de todo eixo . Então fica assim:
Agora vamos ver seu esboço:
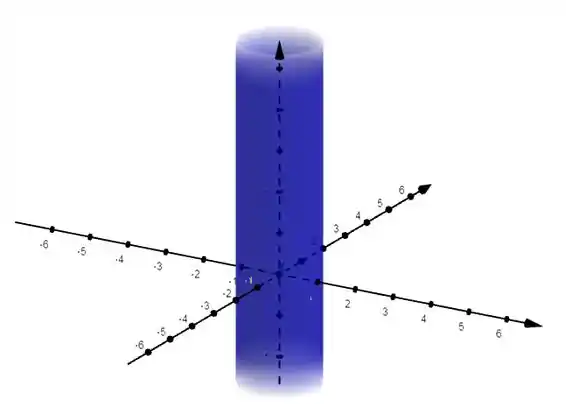
Deste modo, podemos definir um cilindro como sendo uma superfície cuja uma de suas variáveis é livre ou irrestrita (ou seja, temos uma variável que não está restrita por nenhuma equação) .
No cilindro acima, a variável é irrestrita, mas também podemos ter as variáveis ou livres. Neste casos veríamos o cilindro “deitado”.
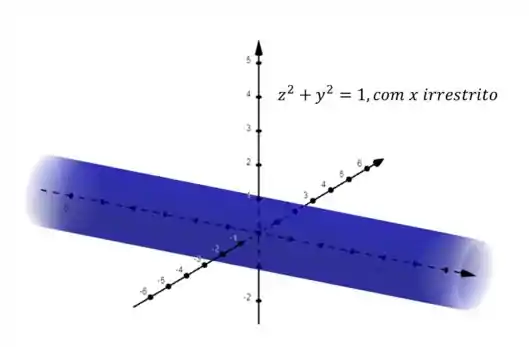
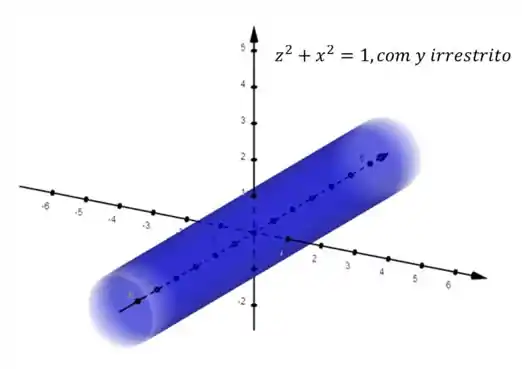
Repara que para saber qual é a variável irrestrita, basta olhar a que não aparece na equação.
Alguns nomes são importantes pra você não ser surpreendido na hora da prova :
- A curva é chamada de diretriz do cilindro . A curva diretriz do cilindro pode ser qualquer curva ou função envolvendo duas variáveis. Ela tem esse nome porque é ela quem define a cara que o cilindro vai ter.
- O eixo do cilindro será o eixo que contém a variável irrestrita.
Sabemos que é a circunferência de raio 1. Se cortarmos o cilindro em seções ortogonais ao eixo z, todas elas serão também circunferências de raio 1.
Observação: Quando falamos em cilindro, na verdade estamos falando em superfície cilíndrica, ou seja a casca cilíndrica. Tá, mas o que isso quer dizer exatamente? Observe novamente o gráfico do cilindro que utilizamos como exemplo inicial. Perceba que o cilindro não compreende o interior da superfície. Ou seja, ele não é maciço, é oco. As interseções com planos ortogonais ao eixo são circunferências e não círculos. Ficou claro agora??
Esboço de Cilindros
Tá, galerinha, até aqui vocês já conheceram a equação e o gráfico, mas agora eu quero te fazer outra pergunta: como fazemos o esboço do cilindro?
Para fazermos o esboço de cilindros, precisamos saber apenas qual a curva diretriz do cilindro e o eixo do cilindro.
Voltemos ao exemplo inicial:
Como vimos, a curva diretriz é e o eixo do cilindro é o eixo .
Agora vamos de um passo a passo!
Passo 1: Esboçar a curva diretriz
Começamos esboçando a curva diretriz no plano
Ela é uma circunferência com centro e raio . Temos:
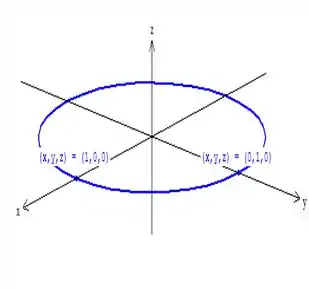
É o mesmo desenho que fiz la no início, mas com outra persectiva.
Passo 2: Empilhar nossos círculos no eixo
Vamos fazer a mesma circunferência mais duas vezes: uma acima e outra abaixo do plano
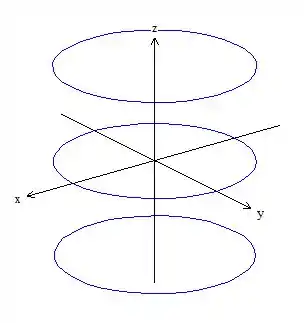
Passo 3: Ligar as circunferências
Fica assim:
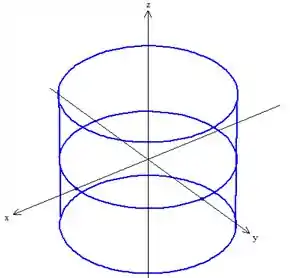
Só um pouquinho de formalismo, pois você ler em algum lugar: essas linhas adcionadas ao longo do eixo do cilindro são chamadas de geratriz do cilindro.
Passo 4: Hachurar a figura.
Agora, é so hachurar a superfície!!! Pronto, tá aí o nosso cilindro!!!
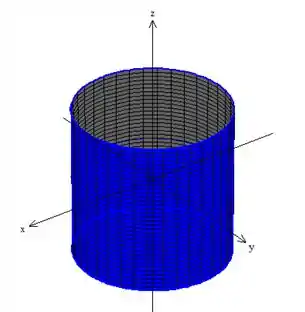
ATENÇÃO! Nem todo cilindro é uma superfície fechada.
Considere o cilindro de equação:
Seu gráfico é:
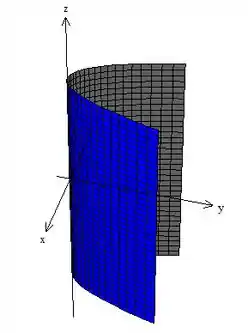
Como você percebeu, os cilindros podem ser aberto! Além disso, a diretriz nem sempre é um círculo, nesse caso foi uma parábola! Só para fechar vou te mostrar outros cilindros
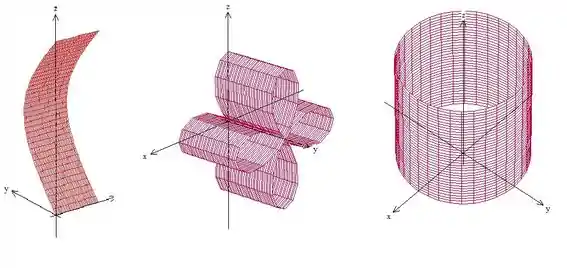
Agora bora pros exercícios!
Esboço de Cilindros
Exercícios Resolvidos
Exercício Resolvido #1
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 58 – 7,8.
Faça um esboço do cilindro de equação dada.
Passo 1
a)Tudo que precisamos saber para esboçar o gráfico de um cilindro é saber qual a curva diretriz do cilindro e qual o eixo do cilindro.
Passo 2
A primeira coisa é entender que curva diretriz é essa.
Isso lembra muito uma circunferência, até porque ele é uma circunferência!
A forma geral da circunferência é
Não precisa ser e , pode qualquer dois entre , e . Lembrando que é o centro da circunferência e é o raio da circunferência. Esse zero é porque a circunferência “está” no plano com , que é a outra variável.
Podemos ver então que o centro vai ser
E o raio vai ser
Portanto, nossa curva diretriz é , que é uma cincunferência de raio e centro . Logo, o eixo do cilindro será o eixo que contém a variável livre, nesse caso o eixo .
Passo 3
Agora que já sabemos qual a curva diretriz e qual o eixo do cilindro, podemos começar seu esboço.
Vamos plotar a curva diretriz no plano .
O gráfico vai ficar:
Passo 4
Como fazemos o cilindro agora? Repita a curva diretriz um pouco mais acima, representando os valores positivos e um pouco mais abaixo, representando so valores negativos. Fica assim:
Passo 5
Vamos colocar retas paralelas(geratrizes) ao outro eixo (eixo do cilindro). Veja essa figura de como fica:
Passo 6
Agora é só hachurar a superfície delimitada pelas figuras. Fica assim:
Passo 7
b)
A primeira coisa é entender que curva é essa.
De novo temos uma circunferência, dessa vez o plano que vamos pegar como base que é diferente. Vai ser o plano .
O centro vai ser
O raio vai ser
Portanto, nossa curva diretriz , que é uma cincunferência de raio e centro . Logo, o eixo do cilindro será o eixo que contém a variável livre, nesse caso o eixo .
Passo 8
Agora que já sabemos qual a curva diretriz e qual o eixo do cilindro, podemos começar seu esboço.
Vamos plotar a curva diretriz no plano .
O gráfico vai ficar:
Passo 9
Agora, vamos repetir a figura, uma mais para trás, representando a parte negativa e uma outra mais para frente, representando a parte positiva. Fica assim:
Passo 10
Como fazemos o cilindro agora? Simples, vamos colocar retas paralelas(geratriz) ao outro eixo(eixo do cilindro). Olha essa figura de como fica:
Passo 11
Hachurando a área delimitada pela figura temos:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Georg B. Thomas, Cálculo Volume 2, 11ª ed. São Paulo: PEARSON, 2008 education do Brasil Ltda, pp. 218 - 67
Esboce o gráfico do cilindro:
Passo 1
A variável irrestrita é e consequentemente o eixo do cilindro é o eixo .
A curva diretriz é a hipérbole
Logo já identificamos os principais elementos para esboçar o gráfico do cilindro.
Passo 2
Vamos esboçar a hipérbole no plano . Temos:
Passo 3
“Expandindo” a hipérbole em direção ao eixo do cilindro temos:
Resposta
Exercício Resolvido #3
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 58 - 15.
Esboce o cilindro:
Passo 1
Encontrar a curva diretriz e o eixo do cilindro.
A curva diretriz do cilindo é a curva , portante a variável irrestrita é e o eixo do cilindro é o eixo .
Passo 2
Agora vamos desenhar a curva , no plano
; ; ;
Portanto temos:
Passo 3
“Expandindo” a curva na direção do eixo do cilindro temos:
Resposta
Exercício Resolvido #4
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 58 - 16.
Faça um esboço do cilindro de equação dada.
Passo 1
A variável irrestrita é e consequentemente o eixo do cilindro é o eixo .
A curva diretriz é
Logo já identificamos os principais elementos para esboçar o gráfico do cilindro.
Passo 2
Vamos esboçar a curva diretriz no plano . A curva diretriz é . Portanto temos:
Passo 3
Depois disso, vamos repetir a curva diretriz, um pouco mais a frente, representando os valores positivos e um pouco mais atrás, representandoos valores negativos. Fica assim:
Passo 4
Agora, vamos colocar retas paralelas(geratrizes) ao outro eixo(eixo do cilindro)
Passo 5
Hachurando a superfície, eis aí o nosso cilindro!
Resposta
Exercício Resolvido #5
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 58 - 17
Faça um esboço do cilindro de equação dada.
Passo 1
Precisamos identifica a curva geratriz e o eixo do cilindro para fazer seu esboço. O eixo do cilindro é o eixo , é o eixo da variável livre, que não aparece na equação. Mas e a curva diretriz ???
Essa curva é um pouco mais complicada, vamos focar um pouco pra entender isso.
Quando temos módulo temos uma situação para o cara positivo e uma situação para o cara negativo.
Vamos considerar primeiro
Isso nos diz que
A função vai ser
O gráfico fica
Passo 2
Vamos ver agora
Isso nos diz que
A função vai ser
O gráfico fica
Passo 3
Vamos ver agora
Isso nos diz que
A função vai ser
O gráfico fica
Passo 4
Vamos ver agora
Isso nos diz que
A função vai ser
O gráfico fica
Passo 5
Juntando essa bagaça toda, vai ficar:
Essa é a nossa curva diretriz do cilindro!!!
Passo 6
Agora devemos desenhar novamente a curva geratriz: Uma mais a frente, representando os valores positivos e outra mais atrás representando so valores negativos. Fica assim:
Passo 7
Desenhando as diretrizes do cilindro temos:
Passo 8
Finalmente, hachurando a superfície temos:
Resposta
