Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Equação da Reta e Segmento de Reta

Ver Todos os Exercícios

Teoria

Retas no Espaço

Para que uma reta esteja definida no espaço, precisamos apenas de duas informações:

  • Um ponto P 0
  • Um vetor que dá a direção da reta (chamamos de vetor diretor v → )

Captou a mensagem?! Olha no gráfico aí pra confirmar !!

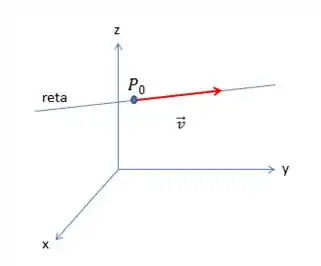
Agora para um segmento de reta, precisamos saber o ponto inicial onde o segmento de reta começa e o ponto final onde o segmento de reta termina.

Pronto! Com isso temos tudo que é necessário para trabalhar com retas e segmento de retas ! É sério, confie em mim!

Equações Paramétricas de Retas no Espaço:

Imagine um vetor (diretor) v → = a , b , c = ( 1,2 , 4 ) e um ponto P 0 = x 0   ,   y 0   , z 0 = ( 1,1 , 1 ) . Queremos encontrar a equação da reta r que passa no ponto P 0 e é paralela ao vetor v → .

Veja a figura a seguir:

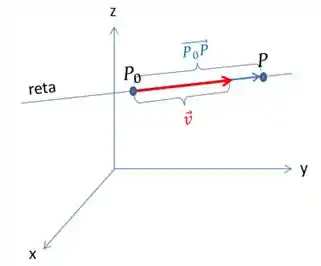
Seja P um ponto qualquer pertencente a reta r →

P = x , y , z .

Como obtemos o vetor P 0 P → ? Basta fazer as componentes de P menos as componentes de P 0 , ou seja:

P 0 P → = ( x - 1 , y - 1 , z - 1 )

Como a reta r é paralela ao vetor v → , e o vetor P 0 P → é formado por dois pontos que pertencem a reta r , então P 0 P → é paralelo a v → . Em termos de componentes, isso significa:

P 0 P → = v → t

x - 1 ,   y - 1 , z - 1 = 1,2 , 4 t

x = 1 + t

y = 1 + 2 t

z = 1 + 4 t

t   ∈ R

A equação da reta fica:

r t = P 0 + v → t

r t = 1 + t ,   1 + 2 t ,   1 + 4 t  

t   ∈ R

Portanto, generalizando, a equação paramétrica da reta que passa pelo ponto P 0 = ( x 0 , y 0 , z 0 ) e é paralela ao vetor v → = ( a , b , c ) será:

r t = P 0 + v → t

r t = x 0 + a t ,   y 0 + b t ,   z 0 + c t  

t   ∈ R

Não se assuste. Chamamos de equação “paramétrica” da reta apenas porque ela depende do parâmetro t . Beleza?!

Exemplo :

Encontre a equação paramétrica da reta que passa pelo ponto ( 1,2 , 3 ) e é paralela ao vetor 3,2 , 1 .

P 0 = 1,2 , 3

v → = 3,2 , 1

Então, basta encontrar a equação da reta conforme a fórmula:

r t = 1 + 3 t ,   2 + 2 t ,   3 + t

t   ∈ R

Tranquilo ?!

Equações Paramétricas de um Segmento de Reta no Espaço:

Precisamos saber onde o segmento de reta começa e onde ele termina. Nada melhor do que um exemplo para ilustrar. Então vamos lá!

Exemplo:

Encontre a equação paramétrica do segmento de reta que passa pelo ponto 1,2 , 3 e é paralela ao vetor 3,2 , 1 , sabendo que o ponto inicial é - 2,0 , 2 e o ponto final é 10,8 , 6 .

P 0 = 1,2 , 3

v → = 3,2 , 1

P i = - 2,0 , 2

P f = ( 10,8 , 6 )

Agora encontramos a equação da reta normalmente conforme a fórmula:

r t = 1 + 3 t ,   2 + 2 t ,   3 + t

Agora se eu deixar t percorrer todos os reais, eu vou ter a reta toda! Eu não quero a reta toda, só uma porção dela. Para eu “cortar” a reta no pedaço que eu quero, eu tenho que dizer quais os valores de t são os que eu vou utilizar.

Então temos que descobrir o valor t 1 que satisfaz o ponto P i e o valor t 2 que satisfaz o ponto P f . Assim vamos ter t   ∈ [ t 1 , t 2 ] , satisfazendo o segmento de reta. OK?!

r t 1 = 1 + 3 t 1   ,   2 + 2 t 1   ,   3 + t 1 = - 2,0 , 2

Isso nos dá o seguinte sistema

1 + 3 t 1 = - 2 2 + 2 t 1 = 0 3 + t 1 = 2

Escolhendo qualquer uma das equações acharemos o valor de t 1 . Vou escolher a terceira equação. Temos:

3 + t 1 = 2

t 1 = - 1

Agora, vamos encontrar t 2 :

r t 2 = ( 1 + 3 t 2   , 2 + 2 t 2 ,   3 + t 2 ) = 10,8 , 6

1 + 3 t 2 = 10 2 + 2 t 2 = 8 3 + t 2 = 6

Escolhendo a terceira equação temos:

3 + t 2 = 6

t 2 = 3

Logo, a equação do segmento de reta é:

r t = 1 + 3 t ,   2 + 2 t ,   3 + t

t   ∈ - 1,3

Posição relativa entre retas:

São basicamente 3 casos possíveis:

  • Retas paralelas: São retas que pertencem ao mesmo plano, porém não possuem ponto de interseção. Imagine que temos uma reta r 1 com vetor diretor v 1 → , e uma outra reta r 2 com vetor diretor v 2 → . Se a reta r 1 é paralela a reta r 2 então v 1 → é paralelo a v 2 → . Ou seja:

    • v 1 → = c v 2 →

    Onde c é uma constante qualquer

    Se as retas não forem paralelas existem duas possibilidades: Retas concorrentes ou reversas.

  • Retas concorrentes: São retas que se interceptam em um ponto. Imagine agora uma reta r 1 com a seguinte equação paramétrica: r 1 t = ( x 1 + a 1 t 1 ,   y 1 + b 1 t 1 ,   z 1 + c 1 t 1 ) e uma reta r 2 t = ( x 2 + a 2 t 2 ,     y 2 + b 2 t 2 ,     z 2 + c 2 t 2 ) . Se r 1 e r 2 são concorrentes, então existe um valores de t 1 e t 2 em que as coordenadas das retas são iguais (ponto de interseção), ou seja:

    • x 1 + a 1 t 1 = x 2 + a 2 t 2 y 1 + b 1 t 1 =   y 2 + b 2 t 2 z 1 + c 1 t 1 = z 2 + c 2 t 2

  • Retas reversas: São retas que não pertencem ao mesmo plano e não possuem ponto de interseção. Logo, não existe um valor de t em que as coordenadas das retas se igualam. (não paralelas nem concorrentes).

Vamos explorar esses conhecimentos nos exercícios? Partiu!!!

Equações Paramétricas de um Segmento de Reta no Espaço:

Posição relativa entre retas:

Exercícios Resolvidos

Exercício Resolvido #1

Georg B. Thomas, Cálculo Volume 2, 11ª ed. São Paulo: PEARSON education do Brasil Ltda, 2009, pp. 207 - 7

Encontre a equação paramétrica da reta que passa por ( 1 , 1,1 ) e é paralela ao eixo z.

Passo 1

Para encontrar a equação da reta precisamos de duas informações:

  • Um ponto P 0 , por onde a reta passa.
  • Um vetor v → , paralelo a reta.

De cara, o problema já nos fornece P 0 = ( 1,1 , 1 )

Passo 2

Agora, precisamos encontrar v →

O problema não diz diretamente qual é o vetor diretor v → . Porém ele diz que esse vetor é paralelo ao eixo z.

Sabemos que um vetor paralelo ao eixo z é o vetor cujas componentes são 0 , 0,1 . Logo, a reta tem a direção desse vetor e , portanto, podemos adotar o vetor v → = ( 0,0 , 1 ) como sendo o vetor diretor.

Passo 3

Agora, basta montar a equação da reta:

r t =   P 0 +   v → t

r t = 1,1 , 1 + 0,0 , 1 t    

r t = 1,1 , 1 + t

t   ∈ R

Resposta

r t = 1,1 , 1 + t

t   ∈ R

Exercício Resolvido #2

Georg B. Thomas, Cálculo Volume 2, 11ª ed. São Paulo: PEARSON education do Brails Ltda, 2009, pp. 207 - 10

Determine a equação paramétrica da reta que passa por ( 2,3 , 0 ) e é perpendicular aos vetores u → = i ^ + 2 j ^ + 3 k ^ e w → = 3 i ^ + 4 j ^ + 5 k ^

Passo 1

Para encontrar a equação da reta precisamos de duas informações:

  • Um ponto P 0 , por onde a reta passa.
  • Um vetor v → , paralelo a reta.

De cara, o problema já nos fornece P 0 = ( 2,3 , 0 )

Passo 2

O problema não fornece diretamente o vetor diretor. Porém a reta deve ser perpendicular ao vetor u → e w → . Logo, temos de encontrar um vetor que seja perpendicular a u → e w → , pois esse será o vetor diretor.

E como encontramos um vetor perpendicular a outros dois vetores??? Isso mesmo!!! Fazendo o produto vetorial entre esse vetores!!!

v → = u → × w → = i ^ j ^ k ^ 1 2 3 3 4 5 = 2 x 5 - 4 x 3 i ^ - 1 x 5 - 3 x 3 j ^ + 1 x 4 - 3 x 2 k ^ = - 2 i ^ + 4 j ^ - 2 k ^

v → = - 2,4 , - 2

Esse é o nosso vetor diretor

Passo 3

Encontrar a equação da reta :

r t = P 0 + v → t

r t = 2 - 2 t ,   3 + 4 t , - 2 t  

t   ∈ R

Resposta

A equação da reta é:

r t = 2 - 2 t ,   3 + 4 t ,   - 2 t  

t   ∈ R

Exercício Resolvido #3

Elaboração Própria

Encontre a equação do segmento de reta que passa pelo ponto P 0 = ( 1 ,   0 ,   2 ) , tem direção do vetor v → = ( 1 ,   0 ,   2 ) entre os pontos ( 2 ,   0 ,   4 ) e ( 4 ,   0 ,   8 ) .

Passo 1

Vamos encontrar a equação da reta que passa pelo ponto P 0 = 1,0 , 2 e é paralela ao vetor v → = 1,0 , 2 . Temos:

r t = P 0 + v → t

r t = ( 1 ,   0 ,   2 ) + ( 1 ,   0 ,   2 ) t

r t = ( 1 + 1 t ,   0 + 0 t ,   2 + 2 t )

r t = ( 1 + t ,   0 ,   2 + 2 t )

Passo 2

Agora vamos descobrir os valores de t 1 e t 2 correspondentes aos pontos dados que determinam o segmento de reta:

Vamos encontrar t 1 :

P i = r t 1 = ( 2 ,   0 ,   4 )

1 + t 1 ,   0 ,   2 + 2 t 1 = ( 2 ,   0 ,   4 )

Temos, então, o seguinte sistema:

1 + t 1 = 2 0 = 0 2 + 2 t 1 = 4

Podemos escolher a primeira equação, ou a terceira equação para encontrar o valor de t 1 . Tanto faz. Escolhendo a primeira equação temos:

1 + t 1 = 2

⇒ t 1 = 1

Agora, falta encontrar t 2 :

P f = r t 2 = ( 4 ,   0 ,   8 )

1 + t 2 ,   0 ,   2 + 2 t 2 = ( 4,0 , 8 )

Temos as seguintes equações:

1 + t 2 = 4 0 = 0 2 + 2 t 2 = 8

Escolhendo a primeira equação temos:

1 + t 2 = 4

⇒ t 2 = 3

Logo:

t ∈ [ 1,3 ]

Resposta

A equação paramétrica do segmento de reta é:

r t = ( 1 + t ,   0 ,   2 + 2 t )

t ∈ [ 1 ,   3 ]

Exercício Resolvido #4

UERJ - Análise Vetorial - Lista Joice - 1e

Obtenha uma parametrização para o segmento de reta que liga os pontos A - 1,0 , 2 e B 2,3 , 3 .

Passo 1

Para encontrar a equação do segmento de reta que liga os pontos A e B , precisamos:

  • Encontrar a equação paramétrica da reta que passa por esses dois pontos
  • Restringir o parâmetro t , para encontrar a equação do segmento de reta que tem como ponto inicial A   ( P i = A ) e ponto final B   ( P f = B ) .

Calma. Vamos fazer passa a passo, bem explicadinho pra você entender.

Passo 2

Para encontrar a equação paramétrica de uma reta precisamos de um ponto P 0 no qual a reta passa, e um vetor diretor v → paralelo a reta.

Vamos adotar o ponto A como sendo P 0 . Então temos:

P 0 = A = ( - 1,0 , 2 )

Passo 3

Agora, falta encontrar o vetor diretor v → , que é paralelo a reta. O problema não fornece diretamente esse vetor.

Porém, repare que podemos usar o vetor A B → , como sendo o vetor diretor v → pois A e B são pontos da reta.Logo, o vetor A B → é paralelo a reta. Então temos:

v → = A B → = 2,3 , 3 - - 1,0 , 2 = ( 3,3 , 1 )

Passo 4

Portanto, a equação paramétrica da reta que passa pelos pontos A e B é:

r ( t ) = P 0 + v → t

r ( t ) = - 1,0 , 2 + ( 3,3 , 1 ) t

r ( t ) = - 1 + 3 t , 3 t , 2 + t

t   ∈ R

Passo 5

Já encontramos a equação da reta, mas o problema pede a equação do segmento de reta que passa por A e B . Então, vamos encontrar os valores de t para os quais P i = A e P f = B .

Temos o seguinte:

P i = r t 1 = A

r t 1 = - 1 + 3 t 1 , 3 t 1 , 2 + t 1 = ( - 1,0 , 2 )

Logo, surgem as seguintes equações:

- 1 + 3 t 1 = - 1 3 t 1 = 0 2 + t 1 = 2

Podemos usar qualquer uma das equações para encontrar o valor de t 1 . Usando a segunda temos:

3 t 1 = 0

t 1 = 0

Agora, só falta encontrar t 2 :

P f = r t 2 = B

r t 2 = - 1 + 3 t 2 , 3 t 2 , 2 + t 2 = ( 2,3 , 3 )

As equações ficam:

- 1 + 3 t 2 = 2 3 t 2 = 3 2 + t 2 = 3

Da segunda equação:

3 t 2 = 3

t 2 = 1

Passo 6

Agora, é só montar a equação do segmento de reta, que é:

r ( t ) = - 1 + 3 t , 3 t , 2 + t

t   ∈ 0,1

Resposta

A equação do segmento de reta é:

r ( t ) = - 1 + 3 t , 3 t , 2 + t

t   ∈ 0,1

Exercício Resolvido #5

George B. Thomas, Cálculo Volume 2, 11ª ed. São Paulo: PEARSON education do Brasil Ltda, 2009, pp. 208 - 61

Determine se as retas tomadas duas a duas são paralelas, se cruzam ou são reversas. No caso de se cruzarem, encontre o ponto de interseção.

L 1 : x = 3 + 2 t ,     y = - 1 + 4 t ,     z = 2 - t - ∞ < t < ∞ L 2 : x = 1 + 4 s ,     y = 1 + 2 s ,     z = - 3 + 4 s - ∞ < s < ∞ L 3 : x = 3 + 2 r ,     y = 2 + r ,     z = - 2 + 2 r - ∞ < r < ∞  

Passo 1

Temos de analisar as retas duas a duas, então vamos começar com as retas L 1 e L 2 . Os vetores diretores são:

v 1 → = 2,4 , - 1 e v 2 → = 4,2 , 4

Vamos verificar se esses vetores são paralelos. Para isso, é necessário que 2,4 , - 1 = c 4,2 , 4 . Temos:

2 = 4 c 4 = 2 c - 1 = 4 c

Precisamos de um valor para c que satisfaça as 3 equações acima simultaneamente. Portanto, vamos resolve-las. Caso as 3 equações forneçam o mesmo valor para c , os vetores são paralelos, caso contrário, os vetores não são paralelos,

Da primeira equação temos:

2 = 4 c

c = 1 2

Da segunda equação temos:

4 = 2 c

c = 2

Da terceira equação temos:

- 1 = 4 c

c = - 1 4

Como os valores para c não são os mesmos, concluímos que os vetores não são paralelos.

Passo 2

Vamos verificar agora se retas L 1 e L 2 possuem um ponto de interseção.

Igualando as coordenadas:

3 + 2 t = 1 + 4 s i - 1 + 4 t = 1 + 2 s i i 2 - t = - 3 + 4 s i i i

Da equação ( i ) temos:

t = - 1 + 2 s

Substituindo o valor de t na equação ( i i ) :

- 1 + 4 - 1 + 2 s = 1 + 2 s →

s = 1 e t = - 1 + 2 ( 1 ) = 1

Agora, vamos verificar se as equações i ,   i i e ( i i i ) são satisfeitas com os valores de s e t encontrados:

Da equação ( i ) :

3 + 2 1 = 1 + 4 1 = 5 ok!!!

Da equação i i :

- 1 + 4 1 = 1 + 2 1 = 3 ok!!!

Da equação i i i :

2 - 1 = - 3 + 4 1 = 1   ok!!!

Portanto as retas L 1 e L 2 são concorrentes e se encontram no ponto ( 5,3 , 1 )

Passo 3

Vamos fazer a mesma análise que fizemos nos passos anteriores, só que dessa vez para as retas L 1 e L 3 .

v 1 → = 1,4 , - 1   ,   v 3 → = ( 2,1 , 2 )

Vamos verificar se os vetores são paralelos, ou seja, se v 1 → = v 3 → c

1 = 2 c 4 = 1 c - 1 = 2 c

Da primeira equação temos:

1 = 2 c

c = 1 2

Da segunda equação temos:

4 = 1 c

c = 4

Da terceira equação temos:

- 1 = 2 c

c = - 1 2

Como os valores para c não são os mesmos, concluímos que os vetores não são paralelos.

Passo 4

Vamos verificar agora se retas L 1 e L 3 possuem um ponto de interseção.

Igualando as coordenadas:

3 + 2 t = 3 + 2 r   ( i v ) - 1 + 4 t = 2 + r   ( v ) 2 - t = - 2 + 2 r   ( v i )

Da equação ( i v ) temos:

t = r

Substituindo o valor de t na equação ( v ) :

- 1 + 4 r = 2 + r

r = 1     t = 1

Agora, vamos verificar se as equações i v ,   v e ( v i ) são satisfeitas:

Da equação ( i v ) :

3 + 2 1 = 3 + 2 = 5 ok!!!

Da equação v :

- 1 + 4 1 = 1 + 2 1 = 3 ok!!!

Da equação ( v i ) :

2 - 1 ≠ - 2 + 2  

Portanto, não há ponto de interseção e as retas L 1 e L 2   são reversas.

Passo 5

Finalmente vamos analisar as retas L 2 e L 3 :

v 2 → = 4,2 , 4

v 3 → = 2,1 , 2

Vamos verificar se os vetores são paralelos:

4,2 , 4 = 2,1 , 2 c

4 = 2 c 2 = 1 c 4 = 2 c

Da primeira equação temos:

4 = 2 c

c = 2

Da segunda equação temos:

2 = 1 c

c = 2

Da terceira equação temos:

4 = 2 c

c = 2

Como os valores para c são os mesmos, concluímos que os vetores são paralelos e as retas L 2 e L 3 são paralelas.

Resposta

As retas L 1 e L 2 são concorrentes e se interceptam em (5,3,1)

As retas L 1 e L 3 são reversas.

As retas L 2 e L 3 são paralelas.