Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Coordenadas Polares

Ver Todos os Exercícios

Teoria

Coordenadas Polares é um negócio esquisito que assusta, né?! Bora aprender de uma vez por todas?!

O que são Coordenadas Polares?

As coordenadas polares são um sistema de coordenadas bidimensional usado para expressar a posição de um ponto. Nele cada ponto do plano pode ser determinado por uma distância e um ângulo em relação a um ponto fixo de referência.

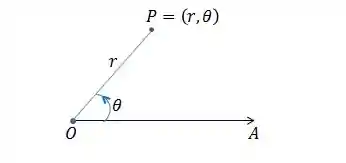
Sistema de coordenadas polares
Sistema de coordenadas polares

Pra aprender TUDO o que você precisa sobre coordenadas polares, pra arrasar na prova, se liga nesse vídeo super completo que o RespondeAí preparou pra você 👇

📢 Clique para saber mais:

Estamos bastante acostumados a utilizar o sistema cartesiano de coordenadas. No sistema cartesiano temos dois eixos: e . As coordenadas de um ponto qualquer são dadas pelas distâncias (com sinal) aos eixos.

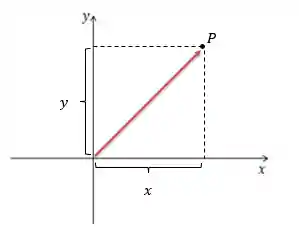
Sistema de coordenadas cartesianas
Sistema de coordenadas cartesianas

Enquanto no sistema de coordenadas polares teremos um único semi-eixo , como indicado abaixo, sendo o ponto conhecido como origem ou polo:

Semi-eixo OA do sistema de coordenadas polares
Semi-eixo OA do sistema de coordenadas polares

Nesse caso, as coordenadas de um ponto qualquer serão dadas pela distância (com sinal) do ponto à origem, chamada de coordenada , e pelo ângulo (medido em radianos) que a distância faz com o semi-eixo , conhecida como coordenada .

OBS.: A coordenada pode se positiva (ponto está acima do semi-eixo ) ou negativa (ponto está abaixo do semi-eixo ). A coordenada também pode ser positiva (ângulo medido no sentido anti-horário) ou negativa (ângulo medido no sentido horário).

Por exemplo, na figura abaixo, qual é a localização do ponto ?

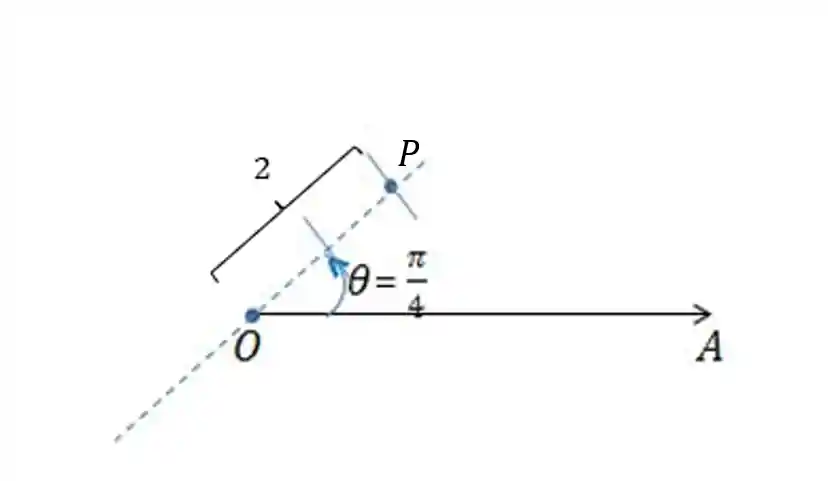
Ponto P representado em coordenada polar
Ponto P representado em coordenada polar

Ao traçarmos uma reta entre a origem do semi-eixo e o ponto temos uma distância de duas unidades e essa reta forma um ângulo de .

Logo podemos escrever:

Quando Usar Coordenadas Polares?

Usamos as coordenadas polares sempre que estamos trabalhando com uma região que apresenta algum tipo de simetria rotacional, nesse caso as coordenadas cartesianas não conseguem descrever tão bem a região.

Coordenadas Polares para Cartesianas

A grande questão é: Como achar as coordenadas polares a partir das coordenadas cartesianas? ou o contrário, como converter as coordenadas polares em coordenadas cartesianas?

Para um ponto com coordenadas cartesianas e e queremos encontrar as coordenadas polares, e , como indicado abaixo:

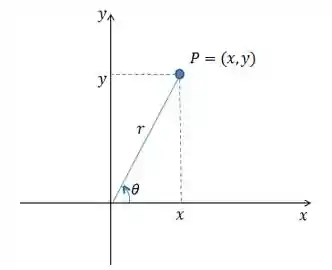
Coordenadas cartesianas e polares de um ponto P
Coordenadas cartesianas e polares de um ponto P

Para descobrir as coordenadas polares basta usar relações trigonométricas, temos:

Perceba que temos um triângulo retângulo, com catetos e e hipotenusa :

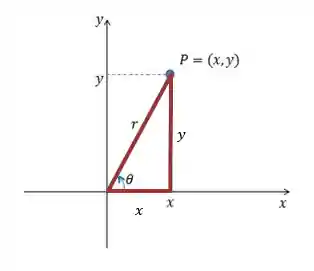
Triângulo retângulo formado pelas coordenadas
Triângulo retângulo formado pelas coordenadas

Assim, podemos dizer que:

ATENÇÃO!! Aqui temos e em evidência, então se quiséssemos achar as coordenadas cartesianas a partir das coordenadas polares usaríamos as relações e .

Mas a nossa intenção é achar as coordenadas polares, então substituímos as equações e na equação :

A partir da expressão acima pode-se encontrar a coordenada .

Usando as razões trigonométricas, temos que:

Substituindo as equações e :

Assim é possível encontrar a coordenada !

Agora você já sabe o que são coordenadas polares e como converter coordenadas polares em cartesianas e vise-versa.

Agora vamos praticar com exercícios!

Quando Usar Coordenadas Polares?

Coordenadas Polares para Cartesianas

Exercícios Resolvidos

Exercício Resolvido #1

Louis Leithold, O Cálculo com Geometria Analítica Volume 1, 3ª ed. São Paulo: HARBRA, 1994, pp. 613 – 21

Ache as coordenadas cartesianas retangulares dos pontos cujas coordenadas polares são dadas:

  1. 3 , π
  2. 2 ,   - 3 4 π
  3. - 4 , 2 3 π
  4. - 1 ,   - 7 6 π

Passo 1

a) Primeira coisa a se fazer é identificar os elementos r e θ . Vamos ter:

r = 3

θ = π

Passo 2

Agora basta utilizar:

x = r . c o s θ

y = r . s e n θ

Substituindo vamos ter:

x = 3 . c o s   π   = 3 - 1 = - 3

y = 3 . s e n π = 3 0 = 0

Passo 3

b) Identificando os elementos r e θ . Vamos ter:

r = 2

θ = - 3 4 π

Passo 4

Agora basta utilizar:

x = r . c o s θ

y = r . s e n θ

Substituindo vamos ter:

x = 2 . c o s   - 3 4 π   = 2 - 2 2 = - 1

y = 2 . s e n - 3 4 π = 2 - 2 2 = - 1

Passo 5

c) Identificando os elementos r e θ . Vamos ter:

r = - 4

θ = 2 3 π

Passo 6

Agora basta utilizar:

x = r . c o s θ

y = r . s e n θ

Substituindo vamos ter:

x = - 4 . c o s   2 3 π   = - 4 - 1 2 = 2

y = - 4 . s e n 2 3 π = - 4 3 2 = - 2 3

Passo 7

d) Identificando os elementos r e θ . Vamos ter:

r = - 1

θ = - 7 6 π

Passo 8

Agora basta utilizar:

x = r . c o s θ

y = r . s e n θ

Substituindo vamos ter:

x = - 1 . c o s - 7 6 π   = - 1 - 3 2 = 3 2

y = - 1 . s e n - 7 6 π = - 1 1 2 = - 1 2

Resposta

  1. - 3,0
  2. ( - 1 , - 1 )
  3. 2 , - 2 3
  4. 3 2 , - 1 2

Exercício Resolvido #2

Louis Leithold, O Cálculo com Geometria Analítica Volume 1, 3ª ed. São Paulo: HARBRA, 1994, pp. 614 – 29

Ache a equação polar do gráfico dada a sua equação cartesiana:

x 2 = 6 y - y 2

Passo 1

Vamos começar usando a relação que conhecemos:

x = r . c o s θ

y = r . s e n θ

Substituindo temos:

r 2 . c o s θ 2 = 6 r . s e n θ - r 2 s e n θ 2

Passo 2

Agora vamos ajeitar essa equação, passando tudo para o mesmo lado e colocando r em evidência:

r 2 . c o s θ 2 + r 2 s e n θ 2 - 6 r . s e n θ = 0

Que é o mesmo que :

r 2 - 6 r . s e n θ = 0

Colocando r em evidência, temos:

r r - 6 s e n θ = 0

Como r ≠ 0 , chegamos ao resultado:

r = 6 s e n θ

Resposta

r = 6 s e n θ

Exercício Resolvido #3

Louis Leithold, O Cálculo com Geometria Analítica Volume 1, 3ª ed. São Paulo: HARBRA, 1994, pp. 614 – 37

Ache a equação cartesiana do gráfico dada a sua equação polar:

r 2 = c o s θ

Passo 1

Vamos começar usando a relação que conhecemos:

x = r . c o s θ

Substituindo temos:

r 2 = x r

O que nos leva a:

r 3 = x

Passo 2

Agora vamos usar a seguinte relação:

r = x 2 + y 2

Então temos:

x 2 + y 2 3 2 = x

Elevando ambos os lados ao quadrado temos:

( x 2 + y 2 ) 3 = x 2

Resposta

( x 2 + y 2 ) 3 = x 2

Exercícios de Livros Relacionados

Escreva uma equação polar de uma cônica com o foco na origem e com os dados fornecidos. P a r á b o l a , v é r t i c ee m4 ,3 π 2 á é
A órbita de Marte em torno do Sol é uma elipse com excentricidade 0,093 e semieixo maior 2,28.10 8k m . Encontre uma equação polar da órbita.
O cometa Hale-Bopp, descoberto em 1995 , tem uma órbita elíptica com excentricidade 0,9951 e o comprimento do eixo maior é 356,5A U . Encontre uma equação polar para a órbita desse cometa. Quão perto
A órbita do cometa Halley, visto pela última vez em 1986 e com retorno esperado para 2062 , é uma elipse com excentricidade 0,97 e com um foco no Sol. O comprimento do eixo maior é 36,18A U . [Uma uni
Usar r0 e- 2 πθ ≤ 0 Para escrever os pontos P 1 3 , - 1 e P 2 - 2 ,- 2 em coordenadas polares.