Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Produto Escalar

Ver Todos os Exercícios

Teoria

Como calcular?

Vou te ensinar aqui como calcular o produto escalar entre dois vetores v → e u → . Tá preparado?

Então se prepara..... que esse é o assunto mais tranquilo ever! Haha

Vamos lá:

Se a gente tem dois vetores v → = ( v 1 , v 2 ) e u → = ( u 1 , u 2 ) não nulos, o produto escalar entre eles é dado por:

v → ∙ u → = ( v 1 u 1 + v 2 u 2 )

A gente lê v escalar u e esse produto é um NÚMERO. Isso mesmo, é um escalar!

Olha como é fácil:

v → = ( 1,2 )

u → = ( 3,4 )

v → ∙ u → = 1.3 + 2.4 = 11

Existe uma forma alternativa de se calcular o produto escalar e ela nos ajuda a descobrir o ângulo entre dois vetores.

Ângulo entre vetores

O produto escalar também pode ser calculado como:

v → ∙ u → = v → u → c o s θ

Sendo v →   e   u → o módulo desses dois vetores e c o s θ o cosseno do ângulo entre os dois vetores.

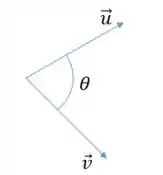
Assim, se a gente quiser descobrir o ângulo entre os dois vetores é só fazer:

c o s θ = v → ∙ u → v → u →     ,       0 ≤ θ ≤ π

De boas, né?

Agora presta toda atenção da sua vida no que vou falar:

Se dois vetores são perpendiculares, então o produto escalar entre eles é nulo.

É fácil perceber isso olhando pra essa segunda forma de calcular o produto escalar que eu te dei: se dois vetores são perpendiculares, θ = π 2 e cos ⁡ π 2 = 0 , logo, o poduto escalar vai ser zero também. Tranquilo, né?

Então, agora se a gente tiver andando na rua e alguém disser “me diz um vetor perpendicular a v → = ( 2,1 ) ” a gente já vai saber o que fazer né? rs

x , y ∙ 2,1 = 0

2 x + y = 0

Ou seja, um vetor perpendicular a v → é um vetor u → = ( x , y ) que satisfaz essa equação ai. Pode ser o vetor u → = ( - 1,2 ) . Ou o vetor u → = ( 1 , - 2 ) .

Tá, agora só mais uma coisinha:

O produto escalar é comutativo. Ou seja, tanto faz se você fizer v → ∙ u → ou u → ∙ v → . O resultado vai ser o mesmo. Pode conferir!

Ângulo entre vetores

Exercícios Resolvidos

Exercício Resolvido #1

George B. Thomas, Cálculo,Volume II,11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009, pg. 239, exercício 16.

r t = 2 2 t , 2 2 t - 16 t 2 é a posição de uma partícula no espaço no instante t . Encontre o ângulo entre os vetores aceleração e velocidade no instante t = 0 .

Passo 1

Antes de mais nada, precisamos encontrar os vetores velocidade e aceleração e substituir em t = 0 :

Velocidade:

v t = r ' t = 2 2 , 2 2 - 32 t

v 0 = 2 2 , 2 2

Aceleração:

a t = v ' t = ( 0 , - 32 )

a 0 = ( 0 , - 32 )

Passo 2

Agora, para descobrir o ângulo precisamos usar a fórmula

c o s θ = v → ⋅ a → v → a →

Então, primeiro vamos calcular esse produto escalar que está no numerador:

v → ⋅ a → = 2 2 , 2 2 ⋅ 0 , - 32 = 2 2 0 - 2 2 32 = 0 - 16 2 = - 16 2

Passo 3

Agora, vamos calcular o módulo de cada um dos vetores:

v → = 2 2 2 + 2 2 2 = 1

a → = 0 2 + - 32 2 = 32

Passo 4

Agora é só substituir:

c o s θ = v → . a → v → a →

c o s θ = - 16 2 1.32 = - 2 2

θ = 3 π 4

Resposta

θ = 3 π 4

Exercício Resolvido #2

UFRJ, Cálculo Diferencial e Integral 2, P12015.1, questão múltipla escolha 7

As curvas C 1 e C 2 parametrizadas respectivamente por

r 1 t = e t 2 - t 2 , sin ⁡ t π , t ∈ R

r 2 s = s - 1 2 + 1 , s , s ∈ R

Passam pelo ponto P = 1,1 . O ângulo formado pelos vetores tangentes às curvas C 1 e C 2 no ponto P é:

a) π

b) π 2

c) π 4

d) π 8

e) π 3

Passo 1

Antes de mais nada, se essas curvas têm o ponto P , então existem os parâmetros t 0 e s 0 tais que:

r 1 t 0 = r 2 s 0 = 1,1

Então, encontremos esses parâmetros!

Igualando r 1 t 0 a 1,1 , temos:

r 1 t 0 = e t 0 2 - t 0 2 , sin ⁡ t 0 . π = 1,1

Pela segunda coordenada, teremos:

sin ⁡ t 0 π = 1

E, pela primeira temos:

e t 0 2 - t 0 2 = 1

Para a exponencial dar 1 o seu argumento deve ser zero.

t 0 2 - t 0 2 = 0

Logo, t 0 = 1 2 !

Da mesma forma, para r 2 , teremos:

s 0 - 1 2 + 1 , s 0 = 1,1

Analisando a segunda equação, temos direto que s 0 = 1 !

Passo 2

Com os valores dos parâmetros a postos, podemos derivar cada curva e ver quais são os vetores tangentes!

Para r 1 , teremos:

r 1 ' t = e t 2 - t 2 . 2 t - 1 2 , π cos ⁡ t π

Que, para t = 1 2 , é:

r 1 ' 1 2 = e 1 2 2 - 1 2 2 . 2 1 2 - 1 2 , π cos ⁡ π 2 = 1 2 , 0

Para r 2 , teremos:

r 2 ' t = 2 s - 1 1 , 1

Colocando s = 1 , teremos:

r 2 ' 1 = 2 1 - 1 1 , 1 = 0,1

Passo 3

Fazendo o produto escalar temos que

r 1 ' 1 2 ⋅ r 2 ' 1 = 1 2 , 0 ⋅ 0,1 = 0

Então eles são perpendiculares! Assim, θ = π 2 :D

Resposta

Letra b

Exercício Resolvido #3

George B. Thomas, Cálculo,Volume II,11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009, pg. 282, exercício 31.

A posição de uma partícula em movimento no espaço no instante t ≥ 0 é

r t = 2,4 s e n t 2 ,   3 - t π

Encontre o primeiro instante em que r ( t ) é ortogonal a ( 1 , - 1,0 ) .

Passo 1

Sabemos que dois vetores são ortogonais se o produto escalar entre eles é nulo. Então:

r t . 1 , - 1,0 = 0

2,4 s e n t 2 ,   3 - t π . 1 , - 1,0 = 0

2.1 - 1.4 s e n t 2 + 0   3 - t π = 2 - 4 s e n t 2 = 0

Passo 2

Temos então

s e n t 2 = 1 2

Agora pensa comigo: rodando no círculo trigonométrico, qual é o primeiro ângulo cujo seno é 0,5 ? π 6 , certo?

Assim:

t 2 = π 6

t = π 3

Resposta

t = π 3

Exercício Resolvido #4

Hamilton Luiz Guidorizzi, Um curso de cálculo, Volume II, 5ª ed. Rio de Janeiro: LTC, 2001, pg.135, exercício 9a.

Suponha v → t ≠ 0 para todo t . Faça T → = v → t v t onde v t = v → t . Prove que T → e d T → d t são ortogonais.

Passo 1

Vamos com calma.

Primeiro vamos fazer

v → t = ( x t , y t )

v t = v → t = x t 2 + y t 2

Até ai tranquilo, né?

Passo 2

Agora vamos substituir isso em T → = v → t v t :

T → = x t v ( t ) , y t v ( t )

Então,

d T → d t = d d t x t v t , d d t y t v t

d T → d t = x ' t . v t - x t . v ' t v t 2 , y ' t . v t - y t . v ' t v t 2

Passo 3

Antes de continuarmos, vamos calcular a seguinte derivada:

d v ( t ) d t = v ' t = x t . x ' t x t 2 + y t 2 + y t . y ' t x t 2 + y t 2 = x t . x ' t + y t . y ' t v t

Beleza, já definimos os vetores e a derivada v ' t . Agora vamos para o que interessa: provar que eles são ortogonais.

Sabemos que dois vetores ortogonais tem produto escalar nulo, então vamos ver se isso acontece aqui:

T → ∙ d T → d t = x t v t , y t v t ∙ x ' t . v t - x t . v ' t v t 2 , y ' t . v t - y t . v ' t v t 2

T → ∙ d T → d t = x t . x ' t . v t - x t 2 . v ' t v t 3 + y t . y ' t . v t - ( y t ) ² . v ' t v t 3

T → ∙ d T → d t = 1 v t 3 v t x t . x ' t + y t . y ' t - v ' t ⏟ x t . x ' t + y t . y ' t v t x t 2 + y t 2 ⏟ v 2 t

T → ∙ d T → d t = 1 v t 3 v t x t . x ' t + y t . y ' t - x t . x ' t + y t . y ' t v t

∴

T → ∙ d T → d t = 1 v t 3 ∙ 0 = 0

Resposta

T → ∙ d T → d t = 1 v t 3 v t x t . x ' t + y t . y ' t - x t . x ' t + y t . y ' t v t = 0