Vetor Binormal
Produzido por Mariana PessanhaTeoria
Interpretação Geométrica
Fala galera! Tudo bem? Nosso foco de estudo agora é o vetor binormal.
Bom, para estudá-lo precisamos nos lembrar de outros dois vetores muito importantes: O vetor tangente unitário e o vetor normal unitário principal . Vamos ver a figura a seguir:
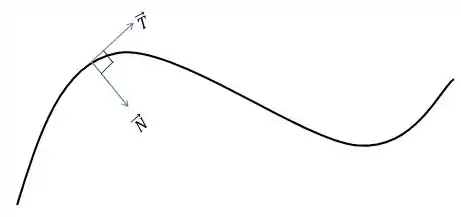
Agora, e se eu te disser que tem um vetor que é ortogonal ao vetor tangente unitário e ao mesmo tempo também é ortogonal ao vetor unitário normal ???
É isso mesmo! E o nome dele é vetor binormal . Ele está representado logo abaixo:
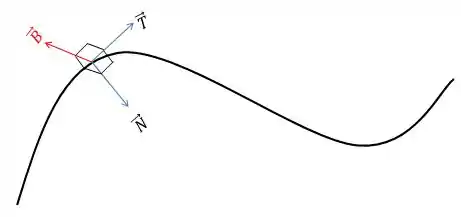
Viu como ao mesmo tempo ele consegue ser ortogonal a e ?! Ainda não? Ele está saindo do plano! Esse trio de vetores e formam o chamado triedo de Frenet ou triedo TNB.
Cálculo do Vetor Binormal
Se o vetor binormal é ortogonal tanto ao vetor tangente unitário, quanto ao vetor normal unitário principal como podemos calculá-lo? Exatamente, fazendo o produto vetorial desses dois vetores!
Então vamos ter:
Repare que como e são unitários, o vetor também será. Vamos ver um exemplo:
Queremos encontrar o vetor binormal a curva:
Passo 1:
Encontrar o vetor tangente unitário
Passo 2:
Encontrar o vetor normal principal unitário
Para isso, precisamos derivar esse vetor e depois dividi-lo pelo seu módulo:
Agora temos:
Passo 3:
Encontrar o vetor binormal
Para isso, vamos fazer o produto vetorial:
Vamos ter
Cálculo do Vetor Binormal
Exercícios Resolvidos
Exercício Resolvido #1
George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009, pp 270 – 1 modificado
Encontre o vetor binormal da curva
Passo 1
Encontrar o vetor tangente unitário:
Passo 2
Encontrar o vetor normal principal unitário
Para isso, precisamos derivar esse vetor e depois dividi-lo pelo seu módulo:
Agora temos:
Passo 3
Encontrar o vetor binormal
Para isso, vamos fazer o produto vetorial:
Vamos ter
Resposta
Exercício Resolvido #2
George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009, pp, 270 – 15, 16
Encontre o valor do vetor binormal no valor dado de
Passo 1
- Encontrar o vetor tangente unitário:
- Encontrar o vetor tangente unitário:
Passo 2
Encontrar o vetor normal principal unitário
Para isso, precisamos derivar esse vetor e depois dividi-lo pelo seu módulo:
Agora temos:
Passo 3
Encontrar o vetor binormal
Para isso, vamos fazer o produto vetorial:
Vamos ter
Passo 4
Portanto, percebemos que o vetor binormal a essa curva independe do instante .
Passo 5
Passo 2
Encontrar o vetor normal principal unitário
Para isso, precisamos derivar esse vetor e depois dividi-lo pelo seu módulo:
Agora temos:
Passo 3
Encontrar o vetor binormal
Para isso, vamos fazer o produto vetorial:
Vamos ter
Passo 4
Já sabemos que
Agora vamos calcular seu valor no instante . Temos