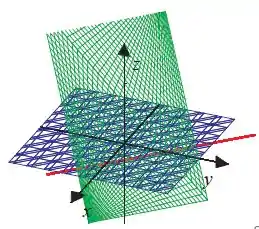
Conjunto de Nível
Produzido por Bruno NeresTeoria
Como calcular?
Imagine que tu chega na sua prova e se depara com uma questão pedindo pra encontrar o conjunto de nível de uma função vetorial, que que você faz?
Chora? Claro que não, afinal, você estuda pelo Responde Aí
Então, você vai saber que para achar o conjunto de nível de uma função vetorial, basta igualar as funções componentes da função vetorial ao nível pedido. Assim, se
O conjunto de nível dessa função é:
Que corresponde a interseção do plano com o plano , que nada mais é que a reta .
Sacou?
É só igualar as funções componentes ao nível pedido e fazer a interseção entre as equações dos planos/superfícies que surgirem.
Tranquilo, né? Então agora se essa questão aparecer na sua prova você vai é ficar feliz, porque é um ponto fácil.
Agora dá uma olhadinha nos exercícios.
Exercícios Resolvidos
Exercício Resolvido #1
UFF, lista 12, Cálculo 2B, exercício 3, itens a e c.
Seja definida por
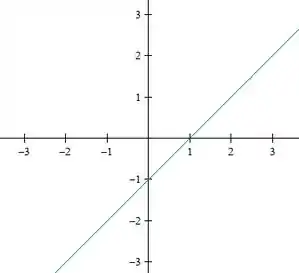
- Faça um esboço das curvas de nível de associadas aos níveis , e .
- Mostre que pertence a curva de nível
De associada ao nível .
Passo 1
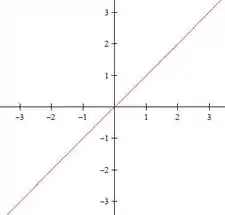
Bom, pra fazer as curvas de nível dessa função, precisamos apenas igualar a função ao nível pedido. Assim, para o nível , temos
Logo, temos a reta
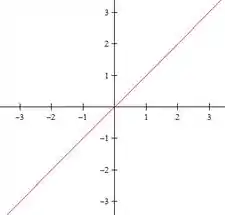
Passo 2
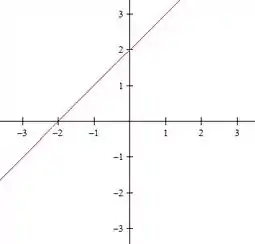
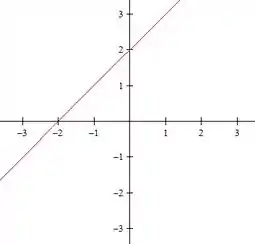
Agora vamos fazer para o nível
Temos então, duas retas:
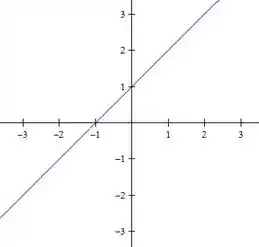
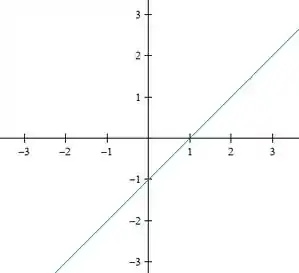
Passo 3
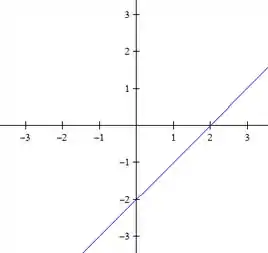
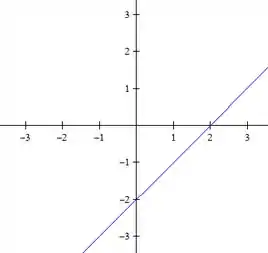
Para o ultimo nível, :
E, over and over again, temos duas retas:
Passo 4
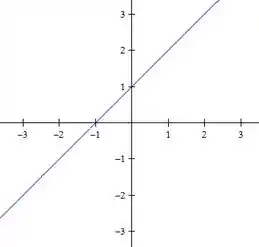
Para mostrar que o ponto pertence a curva de nível dessa função é só substituir esse ponto na função e vê se dá zero
Ou seja, o ponto pertence a curva de nível zero da função.
Repare que apenas olhando para a expressão que encontramos para o nível na letra
Já vemos que o ponto pertence a essa curva.
Resposta
Exercício Resolvido #2
UFF, Cálculo 2B, parte 1,, exemplo 1.2.11.
Determine o conjunto de nível zero da função
Passo 1
Para saber o conjunto de nível dessa função, precisamos apenas igualar a função ao nível pedido. Assim, para o nível , temos
Que é um paraboloide.
Resposta
Exercício Resolvido #3
UFF, Cálculo 2B, parte 1,, exemplo 1.2.5.
Determine e esboce o conjunto de nível da função
Passo 1
Para saber o conjunto de nível dessa função, precisamos apenas igualar as funções componentes ao nível pedido. Assim, para o nível , temos
Assim, o conjunto de nível é
Passo 2
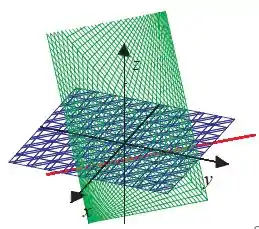
Para esboçar esse conjunto de nível, observe que ele será a interseção do plano
Com o plano
Que nos dá uma reta no plano
Resposta
Reta