Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Gráfico de Funções Vetoriais

Ver Todos os Exercícios

Teoria

O que é?

Em funções de uma variável, quando fazíamos o gráfico de uma função, a gente pegava os valores de x do domínio da função e de f ( x ) da imagem da função e colocava no plano cartesiano ( R ² ), certo?

Aqui em funções vetoriais, a gente faz a mesma coisa.

Dada uma função que leva o vetor

X = x 1 , x 2 , … ,   x n ∈ R n

Em

F X = f 1 x 1 , x 2 , … ,   x n ,   f 2 x 1 , x 2 , … ,   x n ,   … ,   f m x 1 , x 2 , … ,   x n ∈ R m

O gráfico dessa função é o conjunto de pares ordenados X , F X , com X ∈ I m ( F ) , em um espaço de dimensão R m + n , que formam F . Assim, F pode ser uma curva, um plano, uma superfície, ou qualquer outra coisa de dimensão m + n .

Mas, como a gente só sabe desenhar até 3 dimensões, vamos parar nas superfícies mesmo. Assim, m + n será sempre menor ou igual a 3.

Ok, mas agora vamos ver um exemplo pra você entender melhor.

F t = ( cos ⁡ t , sen ⁡ t )

Temos que

X = t ∈ R

F X = F t = ( cos ⁡ t , sen ⁡ t ) ∈ R ²

Assim, o gráfico de F vai ser algo de dimensão 1 + 2 = 3 , que nada mais é que uma superfície.

Agora vamos descobrir que superfície é essa. Como o gráfico é o conjunto de pontos ordenados X , F X , temos:

G F = t , cos ⁡ t , sen ⁡ t ∈ R ³

Agora, para esboçar esse gráfico, temos que ver que

x t = t

y t = cos ⁡ t

z t = sen ⁡ t

Isso tá te lembrando alguma coisa? Não? Então olha só:

Se fizermos y 2 t + z ² ( t ) teremos c o s 2 t + s e n 2 t = 1 . Assim, isso é a parametrização de um círculo, no plano y z , de raio 1 e centro na origem.

Beleza, mas eu disse que o gráfico tem 3 dimensões. Até agora só usamos duas, né? Então agora entra o x t = t . Isso significa que a medida que t cresce, x vai aumentando. Assim, o que temos na verdade é uma espiral ao longo do eixo x .

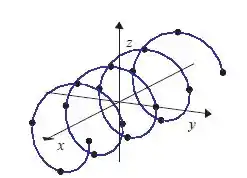
Pegou a ideia?

Dá uma praticada lá nos exercícios agora então.

Exercícios Resolvidos

Exercício Resolvido #1

UFF, Cálculo 2B, parte 1,, exemplo 1.2.6.

Determine e esboce o gráfico da função

F t = ( t , t ² )

t ∈ R

Passo 1

Nesse caso, temos que

X = t ∈ R

F X = F t = ( t , t ² ) ∈ R ²

Assim, o gráfico de F vai ser algo de dimensão 1 + 2 = 3 , que nada mais é que uma superfície.

Passo 2

Agora vamos descobrir que superfície é essa. Como o gráfico é o conjunto de pontos ordenados X , F X , temos:

G F = t , t , t ² ∈ R ³

Agora, para esboçar esse gráfico, temos que ver que

x t = t

y t = t

z t = t ²

Assim, o gráfico será a interseção do plano

x = y

Com o cilindro

z = y 2

Ou

z = x 2

Que dá no mesmo já que x = y .

Passo 3

Portanto, temos uma curva no espaço (lembra que eram 3 dimensões?)

Resposta

Exercícios de Livros Relacionados

Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro t cresce. r t = t ,2 - t ,2 t
Encontre uma equação vetorial e equações paramétricas para o segmento de reta que liga P e Q. P 0 , - 1,1 , Q 1 2 , 1 3 , 1 4
Desenhe as projeções da curva nos três planos coordenados. Use essas projeções para ajudá-lo a esboçar a curva. r t = t , sen ⁡ t , 2c o st
Determine a função vetorial que representa a curva obtida pela interseção das duas superfícies. z = x 2 - y 2 x 2 + y 2 = 1
(a) Esboce o gráfico da curva plana com a equação vetorial dada.(b) Encontre r ’ ( t ) (c) Esboce o vetor posição r ( t ) e o vetor tangente r ’ ( t ) para o valor dado de t . r t = t 2 , t 3 ,t = 1