Curvas Abertas
Teoria
Revisão - Teorema de Stokes
Seja uma superfície orientada, se é um campo vetorial de classe (sua primeira derivada é contínua) e se a fronteira de , que chamaremos de está orientada positivamente, pelo Teorema de Stokes:
Ou seja, usamos o teorema de Stokes geralmente quando encontramos uma integral de linha difícil de ser calculada mas que possua um rotacional mais tranquilo. A fórmula do rotacional é essa aqui
Curvas Abertas
Já vimos que o Teorema de Stokes é usado para uma superfície que possua como fronteira uma curva fechada! Mas e se a fronteira for uma curva aberta e mesmo assim percebermos que pela teorema de Stokes a questão seria muito fácil? Um exemplo é um campo que tenha , iria ser moleza, né?
Neste caso podemos fechar a curva! Uma curva fechada tem o seu final coincidente com o início. Ué, e pode fazer isso? Pode! Desde que façamos uma pequena alteração na fórmula do teorema.
Se temos uma curva aberta qualquer , para aplicar o teorema de Stokes temos que fechá-la com uma curva gerando uma superfície
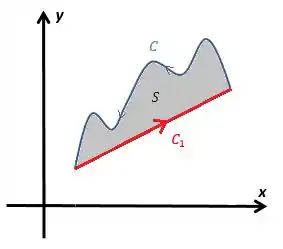
Dessa forma o teorema de Stokes fica
Bem simples, né? Perceba que deve ser a fronteira , portanto essa soma de integrais de linha volta para o teorema original de Stokes
O que fizemos, no final das contas, foi só utilizar um artifício matemático pra conseguir usar o teorema mesmo com a curva aberta.
Algumas observações importantes aqui:
1ª Obs: A integral de linha da curva deve ser simples de calcular! Não adianta nada fazer tudo isso pra ainda ter que calcular uma integral difícil, não é?
2ª Obs: Você pode fechar uma curva com quantas curvas você achar necessário, só lembre-se que teremos que calcular todas essas integrais de linha, então escolha bem qual curva usaremos pra fechar!
3ª Obs: E por fim, para termos uma resolução simples é essencial ter um rotacional bem fácil de integrar! Caso não seja também não vale a pena usar o teorema de Stokes.
Vamos ver um exemplo de uma questão que fica muita tranquila se fecharmos a curva e usarmos o teorema de Stokes
Exemplo: Calcule a integral de linha onde é a interseção do cilindro com o plano no intervalo e
Antes de mais nada, vamos fazer um esboço dessa curva
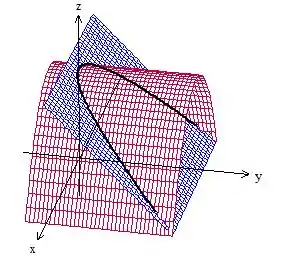
Veja que nossa curva aqui é aberta e, teoricamente, não poderíamos usar o teorema de Stokes aqui. Mas porque tentar fechar a curva só pra usar esse tal teorema? Não vai dar muito mais trabalho? Essa é a pergunta chave! Nesse caso aqui fechar a curva facilita muito, olha o rotacional desse campo
Perfeito, não é? Com o rotacional nulo, aquela integral dupla do teorema de Stokes fica igual a zero!
Bom, essa é a primeira parte pra valer a pena fechar a curva, a segunda observação que devemos fazer é procurar uma curva simples pra fechar a tal curva, uma reta geralmente é uma boa escolha, nesse caso aqui
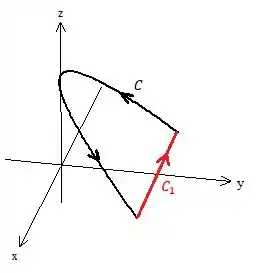
Perceba que o enunciado nos deu a curva no intervalo de , portanto o sentido que escolhemos para a nova curva deve ser tal que se forme uma superfície orientada.
Vamos voltar para o enunciado, as extremidades da curva são os pontos em que
Portanto a reta nada mais é a que liga até e podemos parametrizá-la como onde , incrivelmente simples, né?
Voltando para o enunciado do teorema de Stokes
Onde , portanto essa integral dupla vale zero!
Só precisamos calcular a integral de linha dessa curva bem mais simples! Vamos finalizar então
Pronto, agora é só voltar teorema de Stokes
Tranquilo, não é? É muito importante perceber quando vale a pena fazer esse macete de fechar a curva, vamos pros exercícios praticar isso pra entender melhor!
Exercícios Resolvidos
Exercício Resolvido #1
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009
Calcule , onde e é a curva obtida como interseção da superfície , , com o plano , orientada no sentido anti-horário quando vista de cima.
Passo 1
Vamos lá, galera, essa é bem parecida com aquela que resolvemos na teoria, né? Primeira coisa que precisamos fazer é esboçar nossa curva pra entender que tipo de problema estamos lidando. A interseção do cilindro com o plano é isso aqui
Portanto estamos lidando com uma curva aberta, o problema é que fazer essa integral diretamente seria muito trabalhoso. Vamos tentar calcular o rotacional pra ver se usar o teorema de Stokes é simples
Beleza, vamos fechar a curva com a reta que liga as duas extremidades e ver como fica o teorema de Stokes
Lembre-se de tomar cuidado com as orientações das curvas! O enunciado pediu a curva com orientação anti-horária quando vista de cima, a orientação correta é essa aí do esboço. O teorema de Stokes fica
Vamos calcular então essa integral de superfície e essa integral de linha pra chegarmos na resposta final, vamos lá?
Passo 2
Como já calculamos o rotacional ali no passo 1, vamos terminar a integral dessa superfície logo. Precisamos parametrizá-la, descobrir o seu vetor normal e integrar tudo, certo? Vamos começar pela parametrização.
A superfície está toda contida no plano , sendo que somente é limitada pelo cilindro , podemos obter uma parametrização explícita pela equação do plano!
Os limites de e obtemos pela projeção da superfície no plano
Essa parábola no plano é obtida pela interseção do plano com o cilindro
Além disso o enunciado diz que , portanto
Portanto os intervalos de e são
Graficamente dava pra perceber isso também, só não tínhamos essa equação bizarra da parábola.
Como agora temos a parametrização, vamos substituir isso no nosso rotacional
Pode estar parecendo meio bizarro, mas o produto escalar dessa cara com a normal vai facilitar um pouco as coisas, prometo!
Passo 3
A normal do plano podemos obter pelo macete de quando a parametrização é explícita, lembra dele? É isso aqui, quando
No nosso caso,
Com essa normal vamos poder zerar o termo do meio do rotacional!
Passo 4
Agora é só substituir na integral de superfície
Agora é só integrar!
Passo 5
Pronto, passou a parte mais chata, essa integral de linha agora vai ser mais tranquila. Ela é uma reta, certo? Vamos ver que pontos ela liga!
Sabemos que as extremidades dela estão no plano . Além disso, essas extremidades são limitadas por , então em uma o valor de é e em outra é . Beleza, agora falta . Podemos ver isso pela equação do plano, afinal essa reta pertence a ele!
Portanto a reta liga os pontos até e podemos parametrizá-la por
Para calcular a integral dessa reta, precisamos da derivada da sua parametrização e do campo escrito conforme o parâmetro , vamos fazer isso agora
Portanto a integral de linha fica isso aqui
Passo 6
Pronto, agora é só voltar para o teorema de Stokes
Resposta
Exercício Resolvido #2
Elaboração Própria
Calcule onde é a curva parametrizada por , e o campo
Passo 1
Vamos lá galera, fazer essa integral de linha diretamente parece impossível, né? Vamos tentar outra estratégia aqui. Perceba que a curva é aberta, ela tem esse formato aqui
Se não podemos calcular direto, vamos tentar fechar essa curva e usar o teorema de Stokes, perceba que o rotacional desse campo é bem simples
Vamos então fechar com a reta que liga as extremidades dessa curva! Assim olha
O teorema de Stokes fica
Precisamos então só calcular a integral dupla e a integral de linha de , vamos lá?
Passo 2
Vamos começar com a integral de superfície, ela é uma superfície contida no plano , certo? Com isso a normal é fácil de ser encontrada! Se você não lembra, a normal de um plano qualquer
No nosso plano , temos que , e , portanto
Lembrando que o rotacional calculado lá no passo 1 é esse aqui
A nossa integral de superfície fica isso aqui então
Que beleza! A área da superfície facilita muito! Perceba que a nossa superfície é metade da área de um círculo de raio ! Portanto
Passo 3
Vamos agora para a nossa integral de linha da curva
Precisamos de uma parametrização dessa reta, não é? Ela liga as extremidades da curva , vamos descobrir quais são esses pontos
Então a nossa reta é constante em e , podemos parametrizá-la como
Beleza, substituindo esses valores no campo ficamos com
A derivada da parametrização é essa aqui
Portanto a integral de linha fica isso aqui
Passo 4
Agora é só voltar lá pro que montamos no teorema de Stokes
Resposta
Exercício Resolvido #3
Elaboração Própria
Calcule onde e é parametrizada por ,
Passo 1
Vamos lá galera, essa curva ai dá pra perceber que é aberta, não é? O esboço dela pode ser meio complicado, mas só de substituir e vemos que o começo e o fim são diferentes
O esboço é esse aqui
Parece meio bizarro tentar fazer essa integral de linha diretamente, né? Vamos ver como é o rotacional de pra ver se vale a pena usar o teorema de Stokes
Perfeito! Com esse rotacional nulo o teorema de Stokes parece ser o método mais simples, não é? Precisamos então fechar essa curva.
Geralmente fechamos a curva com uma reta que ligue as duas extremidades. Nessa questão aqui, a reta que liga esses dois pontos é um pouco complexa. Vamos ver que fechar com duas retas mais simples fica mais fácil, olha só
Isso pode ser feito porque o rotacional é nulo! Então não precisamos nos preocupar com a integral da superfície gerada. Só pra deixar claro, varia só no eixo e varia só no eixo
O teorema de Stokes fica assim
Passo 2
Vamos começar então com a reta , vamos precisar de uma parametrização para calcular essa integral. Depois é só calcular o campo em função dos parâmetros e jogar na integral.
A reta vai do ponto até o ponto , certo? O vetor direção é essa aqui
Podemos parametrizar essa reta como
O campo com os novos parâmetros fica
Agora é só jogar esse valor na integral, junto da derivada da parametrização
Passo 3
Vamos para a próxima curva, seguindo o mesmo passo a passo. Precisamos primeiramente da parametrização da reta que vai do ponto até o ponto . O vetor direção é esse aqui
A parametrização fica
O campo com os novos parâmetros fica
A integral vai ficar isso aqui
Passo 4
Beleza, agora é só voltar pro teorema de Stokes