Singularidade

Vamos procurar alguma singularidade, olha a fração! Já vamos desconfiar que pode existir alguma coisa aí!

O demoninador da fração é , então vamos igualar ele a zero:

Para isso devemos ter

Então existe uma singularidade de eixo, eixo . Não podemos usar nenhuma superfície que tenha intercessão com o eixo .

A superfície mais fácil de calcular a integral de linha seria o círculo limitado por , mas esta superfície passa pelo ponto , que é um ponto de singularidade.

Então vamos pegar uma coroa circular limitada pelas curvas e . Agora vamos analisar as orientações, como está no sentido anti-horário, pela regra da mão direita a normal aponta para o sentido positivo de .

A nova curva, , para seguir a mesma orientação deve estar no sentido horário! Veja a figura:

Aplicando o teorema de Stokes nesta superfície teremos:

Calcular o rotacional do campo,

Tempos,

Logo,

Calcular a integral de linha da curva ,

Parametrização de :

Assim,

Como ela está no sentido horário,

Por último vamos substituir os resultados dos passos 4 e 5 na equação resultante do teorema de Stokes!

Como foi pedido na questão!

Podemos resolver está integral pela definição de integral de linha! Veja,

Assim, o promeito passo é parametrizar a curva : e . Como é uma circunferência de raio igual a , pode ser parametrizada por:

Vamos calcular a integral,

Usando a relação fundamental da trigonometria ,

Antes de tudo vamos fazer um gráfico da região para entender melhor a questão. Temos um cilindro com centro cortado por um plano:

Esse desenho não precisa de precisão nenhuma, ok? É só para termos uma ideia mesmo, você pode desenhar um plano qualquer cortando o cilindro.

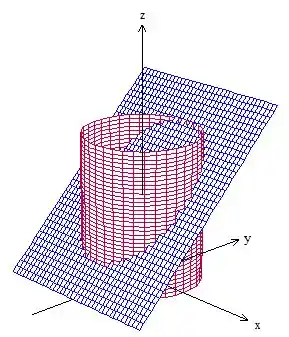
A questão pede para calcularmos a integral de linha em , que é a interseção do plano inclinado com o cilindro. Como podemos ver, forma uma elipse. Percebeu?

Ok, agora vamos analisar o problema. Reparou que a expressão do campo não é nem um pouco amigável, né? Imagina ainda substituir uma parametrização nisso aí, sem condições. Então vamos simplificar as coisas.

O Teorema de Stokes nos diz isso aqui:

Ou seja, podemos substituir essa integral de linha sobre a curva por uma integral do rotacional de sobre uma superfície que tenha a curva como fronteira. Ah, vamos usar o próprio retalho do plano em forma da elipse, né?

Agora vem o momento em que temos que tomar muito cuidado, olha a expressão do campo de novo:

Repare temos uma indeterminação quando e , portanto, o campo não está definido no eixo de simetria do cilindro.

Então, não podemos usar o plano como superfície, na verdade, não podemos usar nenhuma superfície que tenha apenas como fronteira por causa disso!

Ferrou, né. Não, vamos usar uma superfície que tenha como uma de suas fronteiras. Em vez de usar o plano, vamos usar esse pedaço do cilindro, que também tem como fronteira.

Então, é o pedaço do cilindro cortado pelo plano e é a própria curva mais a borda debaixo do cilindro (uma circunferência).Temos então:

Agora vamos pensar nas orientações. Se está no sentido anti-horário, pela Regra da Mão direita, deve ter vetor normal apontando para dentro. Consequentemente, gira no sentido horário.

Precisamos, então, calcular , sabendo que

Temos:

Agora precisamos parametrizar para encontrar seu vetor normal. Temos o cilindro cortado pelos planos e , portanto, .

Bom, como se trata de um cilindro de raio , vamos usar coordenadas ciliíndricas (deslocadas) com :

O que nos dá a parametrização

Onde

E, como temos uma volta completa, .

Agora, vamos calcular a normal:

A normal fica

Levando para a integral:

Onde é dado por

Simplificando a integral

Show?

Agora, para terminar a questão, precisamos calcular a integral de linha na outra borda da superfície, .

Como a circunferência está no plano , sua equação é a mesma do cilindro:

Parametrizando isso aí em coordenadas polares deslocadas com , temos:

Como temos uma volta completa no sentido horário, vai de a .

Essa última componente é porque a curva está no plano .

Certo, agora vamos derivar isso aí:

Agora vamos escrever o campo nas variáveis da parametrização e usar a fórmula:

Levando para a integral, temos:

Temos então

Bom, vamos começar fazendo um esboço dessas superfícies para entender a questão. Temos um parabolóide elíptico virado para baixo com máximo em cortado pelo cilindro de parábola perpendicular ao plano :

A curva do problema é essa formada pela interseção entre as duas superfícies. Para encontrar a sua expressão, vamos igualar as duas equações:

Uma elipse no plano .Mas isso é só a projeção da curva nesse plano, falta a coordenada , que pode ser dada tanto pela equação de uma superfície como a de outra. Vamos escolher a mais fácil, né:

Então, nossa curva vista de cima é uma elipse: guarde essa informação.

Ok, agora vamos analisar o problema. Reparou que a expressão do campo não é nem um pouco amigável, né?

Imagina ainda susbstituir uma parametrização nisso aí, sem condições. Então vamos simplificar as coisas.

Repara que os termos e são bem parecidos. Se a gente separar esse campo vetorial em duas partes (sendo uma delas apenas com essas parcelas), conseguimos um campo conservativo. Olha só:

Beleza? Então, podemos escrever:

Ou seja, primeiro vamos resolver separadamente o problema aplicando Stokes só com o campo , que é conservativo, depois só com o e, então, somar as respostas.

Para o campo

Vamos aplicar Stokes para trocar a integral de linha por uma de superfíce. Ecolhemos como superfícies esse retalho do paraboloide cortado pelo cilindro de parábola (a parte que fica abaixo do cilindro). Então:

Porque não escolhemos a parte de cima do paraboloide? Porque, se você reparar, o campo não está definido quando , ou seja, ao longo do eixo . Então, precisamos de uma superfície que não corte esse eixo!

Bom, mas essa superfície que escolhemos tem duas curvas como borda: em cima, (o que queremos) e embaixo uma elipse no plano , que vamos chamar de . Então, sendo :

Se gira no sentido anti-horário (no plano ), então, para termos orientação positiva, pela Regra da Mão Direita, tem vetor normal apontando para dentro e, consequentemente, gira no sentido horário.

Beleza, agora vamos calcular o rotacional desse campo:

Ainda bem que deu zero né, gente. Ótimo. Então, podemos escrever:

Precisamos agora calcular a integral de linha na elipse . Como é a base do paraboloide, para encontrar sua equação, “cortarmos” ele com o plano :

Tá, ferrou. Quando a gente parametrizar isso aí e substituir a parametrização no campo vai ficar uma porcaria, impossível de integrar. E agora?

Senta que agora vem a bruxaria. Lembra que no início da questão, nós vimos que a nossa curva, vista de cima, era uma elipse de equação ? Pode voltar lá pra checar, eu espero.

Então, se tem essa projeção, quer dizer que ela pertence ao cilindro , não é? Cilindro esse que não corta o eixo ... Agora olha a expressão do campo de novo.

Percebeu que é proporcional a ? Vamos então mudar a nossa superfície, você já vai entender o por que.

Vamos escolher esse cilindro de base elíptica, que tem como bordos a nossa curva e a sua base elíptica . Ou seja, temos isso aqui:

A superfície passa a ser então a parte desse cilindro verde que está entre a curva (em cima, orientada no sentido anti-horário) e a elipse (na base, orientada no sentido horário).

Isso não muda nada para o que fizemos até agora! Isso aqui continua valendo:

Então, precisamos da integral de linha em . Vamos parametrizar usando coordenadas elípticas:

Lembra que a curva pertence ao plano .

Como temos uma volta completa no sentido horário, vai de a zero. Agora vamos derivar essa parametrização:

Agora vamos reescrever o campo em termos da parametrização:

Agora olha que coisa linda que vai acontecer:

Pra isso que servia o cilindro, pra simplificar o denominador do campo, percebeu? Agora vamos substituir tudo o que encontramos nessa fórmula aqui e finalmente calcular a integral de linha da primeira parte do campo em :