Exercícios de Teorema de Stokes em Curvas Abertas - Lista de Exercícios Resolvida
Questão 2
Calcule , onde e é a curva obtida como interseção da superfície , , com o plano , orientada no sentido anti-horário quando vista de cima.
Ver solução completaQuestão 5
Calcule a integral do campo vetorial ao longo da curva interseção da superfície , com o plano , orientada no sentido de crescimento de .
Ver solução completaQuestão 6
Calcule a integral de linha vetorial , onde
E é a intersecção, no primeiro octante, do cilindro e com o plano , do ponto inicial até o ponto final . (Obs.: e
Ver solução completaQuestão 7
Use o teorema de Stokes para Calcular o trabalho do campo
ao longo da curva parametrizada por com .
Ver solução completaQuestão 8
(Cap.16.8 - Exercício 1) Um hemisfério e uma porção de um parabolóide são mostrados. Suponha que seja um campo vetorial sobre cujas componentes tenham derivadas parciais contínuas. Explique por quê
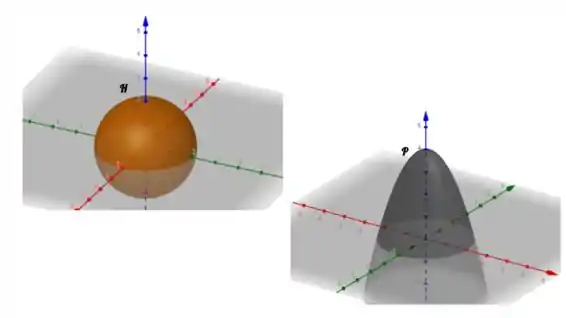
Questão 9
Questão 2: Seja a superfície contida no elipsoide de equação implícita e acima do plano e seja
Um campo espacial.
- Mostre que , a curva na fronteira de , está contida na superfície de equação .
- Calcule .
- Considere que é orientada de modo que sua projeção no plano é percorrida no sentido anti-horário e calcule o trabalho do campo ao longo de .
Questão 10
Seja a curva em parametrizada por . Seja
um campo vetorial em . Calcule a integral de linha do campo vetorial ao longo de .
Ver solução completaQuestão 11
Calcule a integral de linha de campo vetorial onde é a curva definida como interseção, no primeiro octante, do cilindro com o plano , e o campo
Escolhe e indique a orientação da curva .
Ver solução completaQuestão 12
A integral de superfície onde S é com e orientada com a normal exterior é
- 0 b) c) d) e)
Questão 13
Considere o campo
O trabalho realizado para deslocar uma partícula ao longo de uma curva lisa e simples contida na esfera com ponto inicial e ponto final é
- b) c) d) e)
Questão 14
Analise as seguintes afirmações sobre o campo
(I) .
(II) e conservativo em seu domínio.
(III) A integral de superfície de sobre qualquer a esfera de raio a é 0.
Podemos afirmar que:
a) todas as afirmações são verdadeiras.
b) apenas as afirmações (I) é (II) s ̃ao verdadeiras.
c) apenas as afirmações (I) é (III) s ̃ao verdadeiras.
d) apenas a afirmações (I) é verdadeira.
e) apenas a afirmações (II) é verdadeira.
Ver solução completa