Cálculo de Áreas
Teoria
A Integral como Área
Até aqui, muito provavelmente você já sabe calcular a área de várias figuras. Como essas aqui, por exemplo:
Agora, imagina que queremos calcular a área azul abaixo:
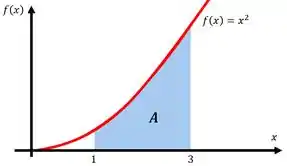
Bom, não tem uma fórmula pra essa área esquisita aí, né!
No caso da figura acima, queremos calcular a área embaixo da função entre e .
Para calcular áreas como essas nós usamos o cálculo da integral definida. Isso porque:
“A integral é geometricamente entendida como a área sob o gráfico da função”
Assim, para encontrar a área da região azul, vamos resolver a integral:
Assim vemos que a área da região azul é unidades de área.
Notação
Podemos generalizar o que fizemos para o cálculo de todas as integrais, uma vez que a integral é entendida como o cálculo da área abaixo do gráfico da função. Assim:

Onde:
é função que descreve o gráfico onde iremos calcular a área;
é o limite inferior, que é onde começa o intervalo da nossa área;
é o limite superior, que é onde termina o intervalo da nossa área; mostra que estamos integrando na variável (se fosse , por exemplo, estaríamos integrando em ).
Assim, calculamos a integral e partimos pro abraço!
Sinal da Integral
Mas espere aí que temos alguns detalhes importantes pra mostrar antes de partir para os exercícios.
Veja, alguns gráficos podem ocupar a parte de baixo do eixo . Isso vai acontecer quando a função for negativa.

Ao calcular a integral de uma função negativa, teremos um resultado também negativo. O que não faz sentido se estamos fazendo um cálculo de área. Então, temos que ter atenção nesse ponto. E se percebermos que naquela região a função está abaixo do eixo , nós colocaremos um sinal de menos na frente da integral. Isso fará com que a área seja calculada corretamente.
E se o gráfico tiver uma parte positiva e outra negativa como no seguinte exemplo?
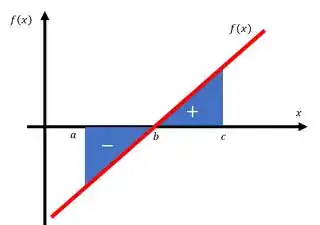
Bom, nesse caso nós teremos que integrar separadamente para que possamos usar o devidos sinais. Então, partiremos nossa integral da seguinte forma:
Fazemos a primeira parte que está abaixo do gráfico, indo de até com o sinal de menos na frente para tornar essa área positiva, e depois fazemos a integral de até , e somamos com a anterior.
Aí sim estaremos considerando toda a região.
Área Entre Curvas
Beleza, já sabemos como calcular áreas através das integrais. Mas e se quisermos calcular a área delimitada por duas funções, como a região pintada do seguinte gráfico:
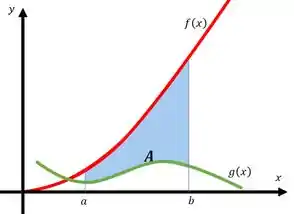
Perceba que a função que está limitando a região por cima é a que é a do gráfico vermelho, e a função que está limitando a região por baixo é a que é a do gráfico verde.
Para calcular a área de região entre as curvas, nós faremos a integral da função de cima, menos a função de baixo.
Assim:
E nesse caso não precisaremos nos preocupar com o sinal das funções caso elas estejam na parte negativa do gráfico, pois a própria construção da integral já fará esse ajuste de sinal.
Agora que já sabemos calcular as áreas sob o gráfico das funções usando o conceito da integral, só o que nos resta é praticar com bastante exercício. Então, partiu!!!
Notação
Sinal da Integral
Área Entre Curvas
Exercícios Resolvidos
Exercício Resolvido #1
Calcule a área determinada pela curva , entre , .
Passo 1
E aí, tudo joia?
Vamos dar uma olhada no desenho dessa área?
Desenhando o gráfico da função e limitando os valores de e , teremos essa região em pintada em verde:
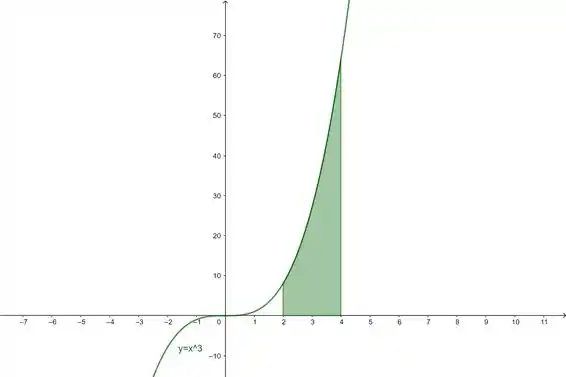
Podemos usar uma integral para calcular essa área:
Que é a integral da curva, no intervalo pedido😉
Passo 2
Vamos resolver essa integral então!
A gente já aprendeu que a integral de uma potência de é isso aqui ó:
Então a nossa é:
Beleza, falta a gente aplicar os limites de integração agora😊
Passo 3
Vamos aplicar os limites, lembrando que a gente faz o resultado do limite maior menos o resultado do limite menor:
Simplificando as frações teremos:
Prontinho! Achamos nossa área, e pra deixar bem bonito a gente acrescenta esse que significa unidade de área! 😊
Resposta
A área determinada pela curva é
Exercício Resolvido #2
Encontre a área da região sob a curva , no intervalo . Interprete geometricamente o resultado.
Passo 1
Opa! Dá uma olhada no esboço dessa área, pra desenhar a região traçamos o gráfico da função , e desenhamos também o intervalo de entre os pontos e .
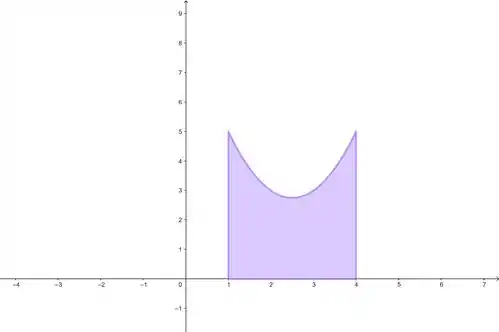
Essa aqui é a intepretação geométrica dela! A voltinha ali é a parábola , e ela está limitada por .
A gente pode calcular essa área fazendo a integral da função no intervalo que foi dado! Ou seja, precisamos calcular isso aqui:
Passo 2
Para resolver essa integral, vamos começar separando essa em outras três, já que nossa função tem três termos:
Lembra que as contantes a gente pode retirar da integral:
E todas essas integrais são de polinômios. Que a gente integral pela regra:
De forma que a integral indefinida é:
Passo 3
Agora a gente tem que substituir os limites de integração:
Lembra que aqui a gente substitui o limite de cima em todos os lugares que tiver na função, e faz a mesma coisa com o limite de baixo, depois subtrai os dois resultados. Assim ó:
Passo 4
Vamos resolver cada potência e arrumar os sinais
A gente pode juntar as frações com denominadores iguais:
Resolvendo as divisões:
Prontinho! Essa é a área da região pedida😉
Resposta
A área da região sob a curva é
Exercício Resolvido #3
Encontre a área da região limitada acima por , abaixo por e nas laterais por e .
Passo 1
Vamos pra mais uma?
Aqui a gente tem duas curvas. O primeiro passo nesse caso é fazer um esboço de cada uma dessas funções no plano.
Começando pelas mais fáceis: e que são só duas retas verticais cruzando esses pontos.
Para fazer o esboço da de forma útil, é uma boa ideia calcular e , e traçar uma reta entre esses dois pontos, já que essa função é uma função linear e seu gráfico sempre será uma linha reta.
E para a também podemos calcular o valor dela nos pontos onde e . O gráfico dessa função é uma parábola, então calculamos que e e fazemos uma parábola razoável que passe por esses dois pontos.
Você deve ficar com algum parecido com isso aqui:
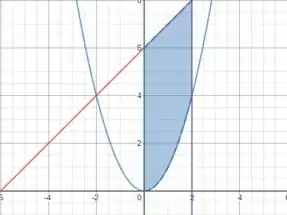
E o nosso objetivo é calcular essa área que está em azul.
Passo 2
Percebe que essa região azul é simplesmente a área embaixo da reta vermelha menos a área em baixo da parábola azul? Tudo isso no intervalo .
Mas “área embaixo da função” é exatamente o que a integral calcula, então escrevendo isso como integrais, vamos achar o seguinte:
Ótimo, agora é só substituir:
Passo 3
E agora ficamos com a integral de um polinômio. Lembra como integra uma função desse tipo? A regra é essa:
Passo 4
Ótimo, agora vamos aplicar essas técnicas para calcular a área:
Show! Agora só falta a gente aplicar os limites de integração...
Passo 5
Pra substituir os limites, a gente faz a substitui o limite de cima em todos os lugares que tem no nosso resultado, faz a mesma com o limite de baixo e subtrai os dois, assim ó:
Repare que o segundo parênteses vai zerar completamente, e ficaremos apenas com:
Resolvendo as potências temos:
Pra somar essa fração, vamos multiplicar o por 3 em cima e embaixo:
Aí agora que as duas frações estão com o mesmo denominador, a gente pode subtrair ali em cima e repetir o denominador:
Pronto, essa é a área da nossa região.
Resposta
A área da região é
Exercício Resolvido #4
Calcule a área determinada pela curva no intervalo .
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala pessoal, tudo joia?
A gente já aprendeu que “Área determinada pela curva” é simplesmente a integral da curva no intervalo dado. Ou seja, temos que resolver o seguinte:
Lembrando que a integral do é . E fica faltando só substituir os limites de integração.
Aplicando os limites de integração teremos o seguinte:
Sabendo que , ficamos com:
Opa, mas isso não está nas opções. Isso significa que essa forma de resolução está ERRADA.
Pois é, é importante lembrar disso. A integral considera que quando a área está abaixo do eixo , ela é uma “área negativa”. Mas quando a questão pede a área, nós não precisamos seguir essa convenção.
Passo 2
Como corrigir esse problema? Bom, a resposta está nessa imagem da nossa curva, se desenharmos o gráfico da função , teremos:
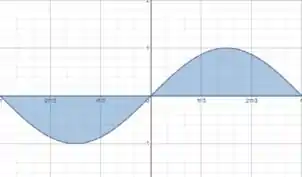
Temos a mesma área dos dois lados, o problema é que a integral “entende” que a área da esquerda é negativa, e isso caba cancelando a integral da direita, levando ao resultado igual a zero, como o que encontramos.
Uma solução pra isso é fazer o seguinte: achar a área em um dos lados e multiplicar por dois!
Ou seja:
E agora que já conhecemos a integral:
Aplicando os novos limites de integração, teremos:
Pronto! Agora sim temos uma resposta coerente, que é a letra A😉
Resposta
- 4
Exercício Resolvido #5
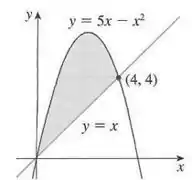
Encontre a área da região sombreada.
Passo 1
Opa! Tudo beleza?
Bom, o exercício pede para acharmos a área da região sombreada! Note que a questão foi legal com a gente e já forneceu o esboço da região.
É importante lembrar que a área entre as curvas é dada pela integral da função que está em cima menos a função que está em baixo.
A função que está em cima é , enquanto a função que está em baixo é . Assim, fazendo a função de cima menos a de baixo, teremos:
Essa será a função que iremos integrar.
Outra coisa que precisaremos é conhecer os limites de integração, e olhando o gráfico podemos perceber que os limites de integração serão e , pois este é intervalo no eixo que delimita a nossa região! Tranquilo? Mãos à obra então!
Passo 2
A área então vai ser dada por:
A gente pode separar essa integral assim:
Ainda podemos retirar a constante pra fora da primeira integral:
E aí a gente vai integrar usando essa regrinha aqui:
Passo 3
Então vai ficar:
Substituindo isso ali em cima, vamos ter:
Podemos simplificar o como , na primeira fração, pra facilitar um pouco as contas:
Show! Vamos aplicar esses limites aí agora😉
Passo 4
A gente aplica os limites fazendo o resultado do limite maior menos o resultado do limite menor. Assim:
Repare que o segundo parênteses vai zera totalmente e só ficaremos com:
Vamos multiplicar o por em cima e embaixo para ficarmos com o mesmo denominador:
Agora a gente pode resolver em cima e repetir o denominador:
E prontinho! Acabamos mais essa😊
Resposta
Exercício Resolvido #6
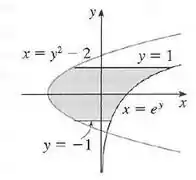
Encontre a área da região sombreada.
Passo 1
Fala aí, bora pra mais uma área?
Perceba que nessa aqui temos funções de , então os intervalos e as variáveis vão ser todas em , beleza?
É como se o nosso gráfico tivesse tombado no eixo .
Seguinte, a área da região limitada pelas curvas é da seguinte forma:
Sendo que como estamos lidando agora com funções de , a gente analisa qual função tá (na frente” e qual está “atrás”.
Concorda que quem tá na frente ali é e quem tá atrás é ? Então, e .
Passo 2
Beleza, falta a gente achar os limites de integração. Vamos olhar em . Nossa figura tá indo de a , certo? Esses são os nossos limites de integração!
Nossa área então é calculada por:
Tirando os parênteses e concertando os sinais, nossa integral se torna:
Podemos separar assim:
Passo 3
Bem, para achar o valor dessa integral vamos calcular a integral indefinida dela e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração.
Agora é fácil achar as primitivas da função, usando quatro expressões da Tabela de Integrais Indefinidas:
Passo 4
Aplicando isso nas nossas integrais, temos:
A gente vai jogar nos limites de integração agora (aí nem vai precisar desse mais)
Passo 5
Agora a gente aplica os limites de integração, lembrando que substituímos o limite de cima em todos os lugares que tiver na nossa função, fazemos a mesma coisa com o de baixo e depois subtraímos os dois. Assim ó:
Agora a gente resolve isso...
Passo 6
Resolvendo as continhas ali...
Tirando os parênteses e concertando os sinais, ficamos com:
A gente pode multiplicar o por em cima e embaixo pra poder somar com o :
Agora já podemos somar em cima e repetir o denominador do :
E pronto! Essa é a nossa área! 😊
Resposta
Exercício Resolvido #7
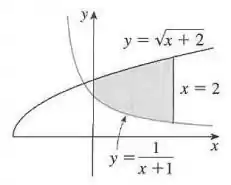
Encontre a área da região sombreada.
Passo 1
Olá, tudo bem?
Precisamos calcular a área da região hachurada (ufa, o enunciado já nos forneceu pelo menos a figura!!!) usando integrais.
É importante lembrar que a área entre as curvas é dada pela integral da função que está em cima menos a função que está em baixo. A função de cima, neste caso, é , enquanto a função de baixo é .
Como a região é limitada à esquerda pelo eixo (reta ) e à direita pela reta , os limites de integração serão e .
Tranquilo até aqui?
Passo 2
Assim, a área pedida será dada por:
Agora vamos achar a integral de cada parte:
Lembrando que , temos que sua integral é
Transformamos o em para podermos somar as frações no expoente e no denominador:
Agora a gente soma em cima e repete em baixo, ficando com:
A fração que está no denominador, nós podemos colocar na frente da função, invertendo ela e deixando ela multiplicando. E o expoente que está fracionário, pode ser escrito em forma de raiz. E ficará assim:
Pronto! Essa foi.
Passo 3
Por outro lado, a integral de é:
Juntando nossas duas soluções, a área é calculada por:
Passo 4
Aplicando os intervalos:
Como , e , segue que
E pronto! Calculamos a área😊
Resposta
Exercício Resolvido #8
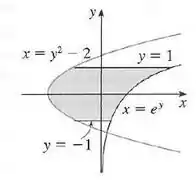
Encontre as áreas da região sombreada.
Passo 1
Fala aí, bora pra mais uma área?
Perceba que nessa aqui temos funções de , então os intervalos e as variáveis vão ser todas em , beleza?
É como se as nossas funções estivessem tombadas no eixo .
Seguinte, a área da região limitada pelas curvas é da seguinte forma:
Sendo que como estamos lidando agora com funções de , a gente analisa qual função tá (na frente” e qual está “atrás”, ao invés de ver qual a que está em cima e qual a que está embaixo.
Concorda que quem tá na frente ali é e quem tá atrás é ? Então, e .
Passo 2
Beleza, falta a gente achar os limites de integração. Vamos olhar em . Nossa figura tá indo de a , certo? Esses são os nossos limites de integração!
Nossa área, então será calculada por:
Tirando os parênteses e arrumando os sinais, a integral se torna:
Podemos separar assim:
Passo 3
Bem, para achar o valor dessa integral vamos calcular a integral indefinida dela e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração.
Agora vamos achar as integrais de cada parte das função, usando quatro expressões da Tabela de Integrais Indefinidas:
Passo 4
Aplicando isso nas nossas integrais, temos:
Então chegou a hora de colocar os limites de integração (aí nem vai precisar desse mais)
Passo 5
Agora a gente aplica os limites de integração, lembrando que substituímos o valor do limite superior em todos os lugares que tiver na função, depois fazemos a mesma coisa com o limites inferior e por fim, subtraímos as duas coisas. Assim ó:
Agora a gente resolve isso...
Passo 6
Resolvendo as continhas ali...
Podemos tirar os parênteses e concertar os sinais, ficando com:
A gente pode multiplicar o por em cima e embaixo pra poder somar com o :
Agora já podemos somar em cima e repetir o denominador do :
E pronto! Essa é a nossa área! 😊
Resposta
Exercício Resolvido #9
Encontre a área da região sombreada.
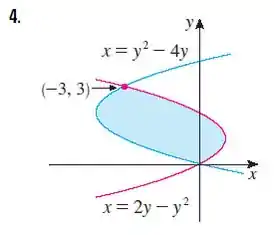
Passo 1
Opaaa! Fala ai! Estamos na reta final de cálculo de áreas
Bom galera, antes de começar, vamos dar nomes aos bois!
A gente tem duas funções em relação a
Começando pela rosinha:
Agora para azul:
Já sabemos como se calcula área sobre as curvas, não é?

Passo 2
Beleza, achamos as curvas, mas e os intervalos de integração?
As curvas se cruzam em dois pontos, . Como nossa variável é o y, nós olhamos qual o menor e o maior valor de . Assim, nosso intervalo de integração vai de
Então temos que
Agora ficou fácil, não é?
Passo 3
Como temos as funções e os intervalos, vamos montar a nossa integral, que é desse jeitinho aqui:
Substituindo as funções:
Agora vamos abrir a equação um pouquinho tirando os parênteses e arrumando os sinais:
Ajeitando essa belezinha aí, ficamos apenas com:
Para ficar mais tranquilinho, vamos separar a integral:
Tiramos a constante da integral:
Agora integrando isso daí, temos:
Podemos simplificar na primeira fração, ficando com:
Aplicando os limites de integração:
Agora, ajeitando isso daí, temos:
Sendo assim:
Resposta
Exercício Resolvido #10
Para quais valores de a reta e a curva delimitam uma região? Encontre a área da região.
Passo 1
Opaaa galerinha, tudo bem? Vamos que vamos!
Bom galera, nesse exercício queremos os valores de para que a reta delimite uma região com a curva especificada.
Utilizaremos depois os conceitos de áreas entre curvas para encontrar a área da região delimitada.
Passo 2
Primeiramente, iremos encontrar os pontos de interseção, igualando os ’s:
Dessa forma, temos
Como temos dos dois lados da igualdade, uma das formas de resolver é fazendo :
De fato, zero é igual a zero e a solução tá certinha, só que pra resolver a questão precisamos dos valores de , então precisamos tentar de outro jeito!
Vamos “cortar” o que está multiplicando os dois lados pra simplificar um pouco a expressão:
Agora podemos resolver:
Se aplicarmos raiz quadrada dos dois lados dessa equação, temos:
Agora, vamos olhar um pouco pra esse resultado que encontramos para entender quais valores de geram soluções válidas.
A forma mais fácil de resolver é quando :
Para qualquer valor de maior que , por exemplo , o primeiro termo da subtração fica menor que o segundo e o resultado passa a ser uma raiz negativa, o que não serve pra gente aqui:
Usando valores de menores que mas ainda positivos, por exemplo , encontramos soluções válidas:
Mas usando valores negativos de , também chegamos a raízes negativas, que não servem aqui:
Dessa forma, deve estar no intervalo para que haja solução.
Passo 3
Utilizando os conceitos de área entre curvas, podemos escrever a seguinte integral
Para simplificar, vamos separar em duas integrais:
Para a primeira vamos fazer uma substituição simples, chamando:
Então ficamos com:
Resolvendo isso, temos:
Mas como o veio da substituição, vamos retornar para termos de :
Agora, vamos resolver a segunda integral:
Apesar dos limites de integração serem complicados, temos apenas uma integral de :
Retornando à expressão completa:
Vamos substituir as duas integrais que resolvemos:
Podemos cortar o que multiplica com os dividindo ambos os termos:
Por fim, substituímos os limites de integração e fazemos as contas:
Resposta
Dessa forma, deve estar no intervalo para que haja solução.
E a área da região será: