Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.7 - Ex. 39
37. Para as funções de uma variável, é impossível uma função continua ter dois pontos de máximo local e nenhum ponto de mínimo local. Para funções de duas variáveis, esse caso existe. Mostre que a função
Só tem dois pontos críticos, ambos de máximo local. Em seguida, utilize um computador para desenhar o gráfico com uma escolha cuidadosa de domínio e de ponto de vista para ver como isso é possível.
Passo 1
Oie, tudo bem? Vamos resolver essa atividade.
Dada a função:
Queremos mostrar que por essa função ser de duas variáveis, podemos ter pontos de críticos de máximo local.
Então precisamos provar que a função só tem dois pontos críticos, a ambos são pontos de máximo.
Já temos nossos pontos de interesse, mas falta dizer se são máximos, mínimos ou pontos de sela, para isso a gente precisa da segunda derivada, vamos usar
Podem ocorrer três casos:
- então é um mínimo local.
- então é um máximo local.
- então não é nem mínimo e nem máximo local.
Então iremos provar aqui a letra b).
Passo 2
Vamos começar fazendo essas derivadas:
Vamos começar fazendo , primeiro vamos separar em duas derivadas
Agora a gente usa a regra da cadeia para ficar mais fácil as derivadas
Onde :
E agora vamos fazer:
De novo usando a regra da cadeia, com :
Então
Agora vamos fazer
Usando a mesma estratégia:
A primeira derivada nem depende de :
E agora vamos fazer:
Agora usando a regra da cadeia, com :
Então:
Passo 3
Beleza, agora a gente já tem nossas derivadas, os pontos interessantes vão acontecer quando elas forem iguais à 0. Então
De a gente pode ver que para aquela equação ser ou ou , então é uma possibilidade.
Vamos substituir em
Isso é uma incoerência, então qualquer ponto onde não é um ponto de interesse.
Agora vamos ver onde . Vamos isolar .
Agora vamos substituir isso em :
Nossa quanto !!! Vamos dar uma simplificada:
Já que temos a condição onde , então a única opção que nos resta é onde , logo .
Assim
Nos pontos
Passo 4
Vamos calcular as segundas derivadas então
Agora derivamos isso em relação a
A outra derivada que precisamos é
Derivando em relação a
E a última derivada que precisamos é
ou
Vamos derivar isso em relação a
Passo 5
Agora vamos verificar a natureza dos pontos críticos.
Vamos testar para o ponto
Então temos que analisar
Então é um ponto de máximo
Agora o ponto
Então temos que analisar
Então é um ponto de máximo também.
Passo 6
Fazendo um gráfico no GeoGebra, temos:
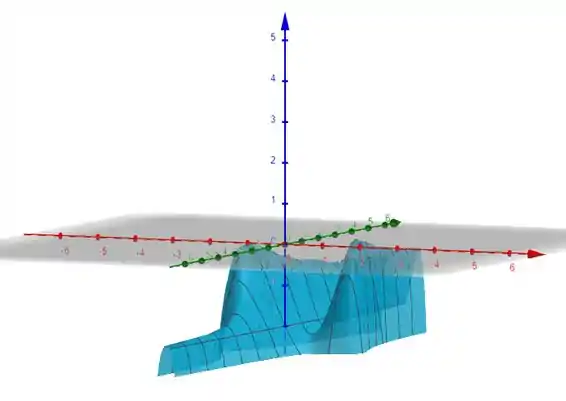
Como é possível verificar os dois pontos de máximo. 😉