Funções de Várias Variáveis

Fala aí, nós somos o Responde Aí, a salvação do seu semestre haha! Nossa missão é ajudar você a arrasar nas suas provas com um estudo direcionado e descontraído.

Hoje vamos te apresentar um assunto bem falado dentro do cálculo, as funções de várias variáveis.

Bom, até esse momento você vem aprendendo sobre as funções de uma única variável, aquelas que relacionam um número , com um outro número :

Por exemplo:

Para cada valor de que nós pegamos, temos um valor de associado, que é calculado através da expressão dada acima. Quando montamos gráficos de funções de uma única variável vemos que eles são uma curva, ou seja, possuem uma única dimensão e em coordenada cartesiana eles estão no plano (2 dimensões):

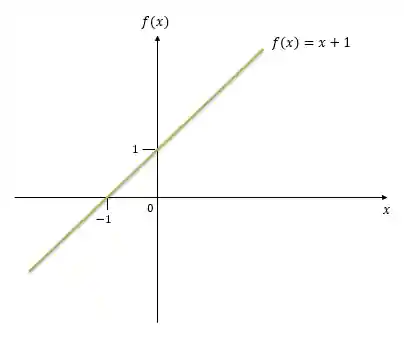
Agora, quando falamos de funções de várias variáveis, estamos falando de funções que relacionam números (, , , ....) a um único número . Para ficar mais claro de entender, vamos considerar um função de duas variáveis. Nesse caso, nós teremos dois números, e , sendo associados a um único número :

Por exemplo:

Para cada par que pegamos, temos um valor associado, que é calculado através da expressão acima, como mostra a tabela abaixo:

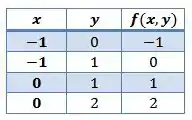
Agora, se formos montar o gráfico de uma função de duas variáveis teremos uma superfície, ou seja, duas dimensões, e nas coordenadas cartesianas eles estarão em três dimensões .

Por exemplo, olha essa função aqui de duas variáveis:

O seu gráfico é o seguinte:

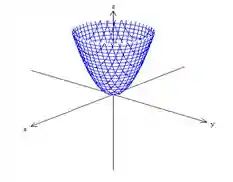
Note que se trata de uma superfície (2 dimensões) e está nas coordenadas cartesianas em 3D.

A gente segue esse mesmo raciocínio para funções de mais de duas variáveis:

• Função de três variáveis - gráfico é um sólido (3 dimensões) e está no plano cartesiano 4D
• Função de quatro variáveis - gráfico é um figura em 4 dimensões e está nas coordenadas cartesianans em 5D.

E assim por diante...

Eu sei que quando começamos a falar de 4 dimensões, 5 dimensões ou até mais a gente não consegue mais imaginar, não é? hahaha Irado!

Essa foi uma breve introdução sobre esse assunto só para você se contextualizar. Se você preferir pode ver essa introdução em um vídeo, que a equipe do Responde Aí preparou 👇🏾

Porém, ainda há muita coisa sobre as funções de várias variáveis que costumam cair em provas. Pensando nisso, nós preparamos um Raio-X, onde temos o conteúdo completo desse assunto listado e organizado em capítulos e tópicos, para o seu aprendizado ser objetivo e eficaz. Confere aqui em baixo 👇🏾