Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.3 - Ex. 60
55-60. Usando a regra de L’Hôpital (Seção 3.6), podemos conferir que:
Com qualquer número real positivo . Nestes exercícios:
a) Use esses limites, se necessário, para obter os limites de quando e .
b) Esboce o gráfico de e identifique todos os extremos relativos, os pontos de inflexão e as assíntotas (conforme o caso). Configura seu trabalho com um recurso gráfico.
60.
Passo 1
a) Então galera, para calcularmos os limites com tendendo a e com tendendo a , caso não haja necessidade de utilizar L’Hôpital, basta aplicarmos os limites, ok? A função que nos foi dada é:
Calculando o primeiro limite, teremos:
Reescrevendo esse argumento, teremos:
E de acordo com o enunciado, temos que:
Então:
Por fim, calculando o segundo limite:
O nosso denominador será um número muito próximo de zero, mas positivo. Já o nosso numerador, temos que o resultado será um número negativo, uma vez que com entre e resulta em um número negativo. Logo:
Ok, a primeira parte foi finalizada! Do resultado que encontramos podemos concluir que nosso gráfico explode para quando a função se aproxima de zero.
Passo 2
b) Caso não se lembre, para identificarmos os pontos de extremos relativos de uma função devemos fazer uma análise dos pontos críticos da mesma, isto é, analisar os pontos em que ou os pontos em que não existe! Ademais, para identificarmos os pontos de inflexão devemos fazer a mesma análise dos extremos, mas agora para , ok? Vamo que vamo!
Derivando a nossa função, teremos:
Igualando nossa derivada a zero, teremos:
Como não pode ser zero, então a única forma disso dar zero é se:
Utilizando a propriedade fundamental de logaritmos:
E esse é nosso único ponto de extremo, galera!
Passo 3
Os pontos de inflexão de uma função são os pontos no qual a função muda de concavidade, ou seja, sai de e vira e vice-versa! Derivando a nossa derivada, teremos:
Igualando a nossa derivada a zero, teremos:
Como não pode ser zero, então a única forma disso dar zero é se:
Utilizando a propriedade fundamental de logaritmos:
Então esse é nosso ponto de inflexão, galera!
Passo 4
Substituindo na nossa função original os valores importantes de que encontramos, teremos:
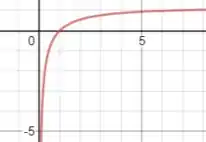
Show! Por fim, plotando o gráfico da função, teremos:
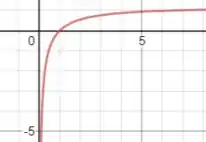
E pelo gráfico notamos que:
O ponto de inflexão está bastante sutil no gráfico, então é normal que esteja sendo difícil de visualiza-lo, mas a questão é que ele existe, e é essa informação que temos que absorver, ok? Show!
E está aí nossa resolução! 😉
Resposta
a)
b) Ponto(s) de extremo(s) relativo(s): ;
Ponto(s) de inflexão: ;
Gráfico:
