Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.3 - Ex. 11
Obtenha um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostre as assíntotas horizontais e verticais e dê suas equações. Identifique (se houver) os pontos em que o gráfico cruza uma assíntota horizontal. Confira seu trabalho com um recurso gráfico.
Passo 1
Vamos lá, aqui como o numerador e o denominador não têm fatores comuns, vamos utilizar alguns passos para facilitar obter o gráfico da função:
Primeiro vamos ver se a função possui alguma simetria em relação ao eixo , vamos substituir por e vamos ver se a equação muda:
A equação mudou, então não temos uma simetria no eixo .
Passo 2
Agora vamos encontrar os cortes com os eixos coordenados fazendo e :
Pronto, sabemos onde que a função corta o eixo o eixo .
Passo 3
Próximo passo é encontrar os valores de com os quais o denominador é igual a zero, nesses lugares o gráfico tem uma assíntota vertical, ou seja, vai aumentando, sempre se aproximando desse valor, mas nunca toca nesse ponto:
Temos então que possui assíntota vertical em .
Passo 4
Próximo passo é analisar o sinal de , vamos analisar os lugares em que pode trocar de sinal, vamos ver os pontos de corte com o eixo e nas assíntotas verticais achando intervalos e analisando se é positivo ou negativo nesses intervalos:
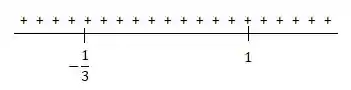
Temos então que a função é toda positiva.
Passo 5
Agora vamos determinar o comportamento no infinito do gráfico calculando os limites de quando e quando , e se algum desses limites tiverem um valor finito , então a reta é uma assíntota horizontal:
Pronto, temos então uma assíntota horizontal em .
Passo 6
Vamos encontrar e :
Fazendo vamos ver se possui algum ponto crítico, onde a derivada é zero, ou onde ela não existe:
Agora vamos usar o Teste da Derivada Primeira:
Se em um intervalo aberto imediatamente à esquerda de e em um intervalo aberto imediatamente à direita de , então tem um máximo relativo em .
Se em um intervalo aberto imediatamente à esquerda de e em um intervalo aberto imediatamente à direita de , então tem um mínimo relativo em .
E se tiver o mesmo sinal tanto em um intervalo aberto imediatamente à esquerda de quanto em um intervalo aberto imediatamente à direita de , então não tem extremo relativo em .
Vamos então analisar as derivadas no intervalo que contém :
Pronto, temos então que e , então tem um mínimo relativo em .
Passo 7
E por último vamos calcular :
Vamos então achar se possui algum ponto de inflexão e analisar os sinais:
Agora vamos analisar o sinal de ao redor de :
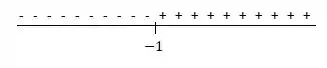
Como trocou de sinal em , temos um ponto de inflexão, onde a concavidade muda de côncava para baixo para côncava para cima.
Passo 8
Pronto, agora com todas essas informações fica mais simples de esboçar o gráfico, vamos lá:
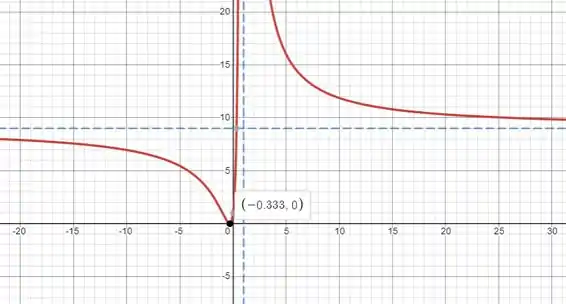
Resposta
