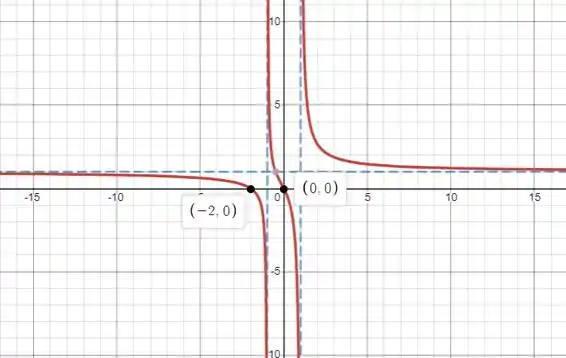
Em cada parte, faça um esboço aproximado do gráfico usando assíntotas e limites apropriados, mas não derivadas. Compare seu esboço ao gerado por um recurso gráfico computacional.
Passo 1
- Vamos lá, aqui como o numerador e o denominador não têm fatores comuns, vamos utilizar alguns passos para facilitar obter o gráfico da função:
- Vamos lá, aqui como o numerador e o denominador não têm fatores comuns, vamos utilizar alguns passos para facilitar obter o gráfico da função:
Primeiro vamos ver se a função possui alguma simetria em relação ao eixo , vamos substituir por e vamos ver se a equação muda:
A equação não mudou, então temos uma simetria no eixo .
Passo 2
Agora vamos encontrar os cortes com os eixos coordenados fazendo e :
Pronto, agora sabemos onde a função corta o eixo e o eixo .
Passo 3
Próximo passo é encontrar os valores de com os quais o denominador é igual a zero, nesses lugares o gráfico tem uma assíntota vertical, ou seja, vai aumentando, sempre se aproximando desse valor, mas nunca toca nesse ponto:
Temos então uma assíntota vertical em .
Passo 4
Próximo passo é analisar o sinal de , vamos analisar os lugares em que pode trocar de sinal, vamos ver os pontos de corte com o eixo e nas assíntotas verticais achando intervalos e analisando se é positivo ou negativo nesses intervalos:
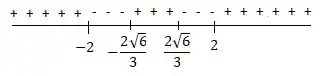
Temos então que nos intervalos e a função é negativa, e nos intervalos , e é positiva.
Passo 5
Agora vamos determinar o comportamento no infinito do gráfico calculando os limites de quando e quando , e se algum desses limites tiverem um valor finito , então a reta é uma assíntota horizontal:
Pronto, temos então uma assíntota horizontal em .
Passo 6
Pronto, agora com todas essas informações fica mais simples de esboçar o gráfico, vamos lá:
Passo 7
Primeiro vamos ver se a função possui alguma simetria em relação ao eixo , vamos substituir por e vamos ver se a equação muda:
A equação mudou, então não temos uma simetria no eixo .
Passo 2
Agora vamos encontrar os cortes com os eixos coordenados fazendo e :
Pronto, agora sabemos onde a função corta o eixo e o eixo .
Passo 3
Próximo passo é encontrar os valores de com os quais o denominador é igual a zero, nesses lugares o gráfico tem uma assíntota vertical, ou seja, vai aumentando, sempre se aproximando desse valor, mas nunca toca nesse ponto:
Temos então uma assíntota vertical em .
Passo 4
Próximo passo é analisar o sinal de , vamos analisar os lugares em que pode trocar de sinal, vamos ver os pontos de corte com o eixo e nas assíntotas verticais achando intervalos e analisando se é positivo ou negativo nesses intervalos:
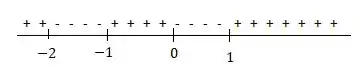
Temos então que nos intervalos e a função é negativa, e nos intervalos , e é positiva.
Passo 5
Agora vamos determinar o comportamento no infinito do gráfico calculando os limites de quando e quando , e se algum desses limites tiverem um valor finito , então a reta é uma assíntota horizontal:
Pronto, temos então uma assíntota horizontal em .
Passo 6
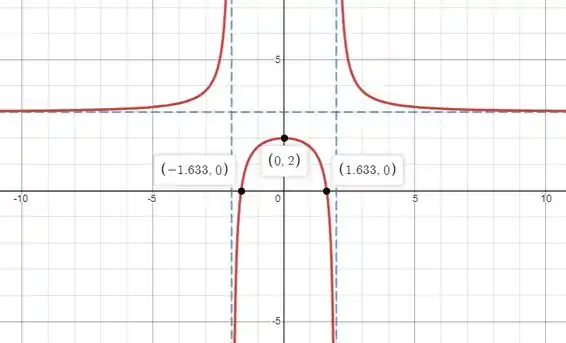
Pronto, agora com todas essas informações fica mais simples de esboçar o gráfico, vamos lá:
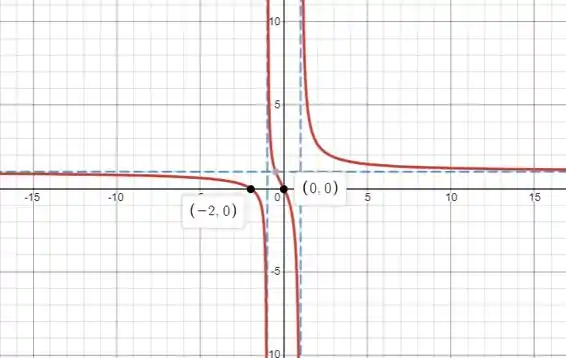
Resposta
a) 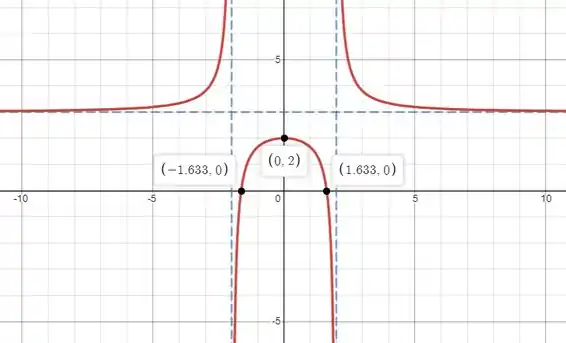
b)