1. Abaixo estão os gráficos de três funções posição. Em cada caso, determine o sinal da velocidade e o da aceleração e, então, se a partícula está aumentando ou diminuindo a velocidade.
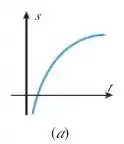
Passo 1
Então pessoal, se observarmos bem o gráfico notaremos que se traçarmos retas tangentes em qualquer ponto, teremos essas retas acima da nossa curva, o que indica uma derivada positiva. Sendo assim, temos que o sinal da velocidade é positivo, ok?
Ademais, notamos que a função está querendo decrescer a partir de um ponto qualquer, não é mesmo? Isso indica que a concavidade da curva é para baixo, ou seja:
Então o sinal da aceleração é negativo.
Por fim, vemos que a curva está crescendo e em um certo momento ela começará a decrescer, não é mesmo? Sabendo disso, podemos dizer que a nossa partícula está diminuindo a velocidade, ou seja, freando!
E essa é a nossa análise da curva em questão, gente!
Resposta
Sinal da velocidade: ;
Sinal da aceleração: ;
Velocidade da partícula está diminuindo.