Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.6 - Ex. 6
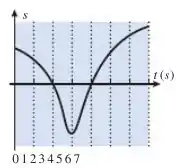
6. A figura abaixo mostra o gráfico de versus para uma formiga movendo-se ao longo de um cano estreito vertical (um eixo com sentido positivo para cima).
a) Quando, se é que ocorre, a formiga atinge a srcem?
b) Quando, se é que ocorre, a formiga está com a velocidade zero?
c) Quando, se é que ocorre, a formiga move-se para baixo?
Passo 1
a) Então galera, isso só ocorre quando a velocidade da formiga é negativa, ou seja, quando . Observando o gráfico temos dois intervalos em que isso ocorre:
O primeiro intervalo ocorre em ;
O segundo intervalo ocorre em .
Passo 2
b) Se observarmos o gráfico com cuidado notaremos que a formiga começa se movendo no eixo negativo do referencial e em um tempo ela para e inverte o sentido do movimento. Exatamente nesse momento em que ela para para mudar o sentido do movimento sua velocidade se anula, e isso ocorre no ponto de mínimo do gráfico, em .
Passo 3
c) Assim como comentado na letra b), a formiga inicia sua trajetória se movendo para baixo, até o momento em que inverte o sentido do movimento, em . Tendo isso em vista, temos que a formiga se move para baixo em .
E está aí nossa análise do movimento da formiga, pessoal!
Resposta
a) O primeiro intervalo ocorre em ;
O segundo intervalo ocorre em .
b) .
c) .