3. Abaixo está o gráfico de uma função posição de uma partícula movendo-se em um eixo horizontal .

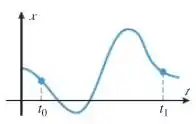
a) A partícula está se movendo para a esquerda ou para a direita no instante ?

b) A aceleração é positiva ou negativa no instante ?

c) A partícula está aumentando ou diminuindo a velocidade no instante ?

d) E no instante , está aumentando ou diminuindo a velocidade?

b) Antes de respondermos a essa pergunta temos que lembrar do seguinte: a derivada da função posição resulta na velocidade e a derivada da fução velocidade resulta na aceleração. Tendo isso em vista, temos que analisar a derivada segunda da função no ponto em questão, beleza?!

Observando o gráfico fica tranquilo de notar que a derivada da função é negativa, assim como a derivada segunda dessa mesma função. Uma derivada segunda negativa implica em uma concavidade para baixo, desse jeito:

Sendo assim, temos que a aceleração é negativa em !

c) Então galera, um pouco antes de vemos que a derivada da função é negativa e a concavidade da função é para baixo, no entanto, após , por mais que a derivada da função continue decrescente, temos que a concavidade da função começa a mudar, o que indica em uma mudança na velocidade. Sendo assim, podemos concluir que a velocidade é positiva em !

d) Nas proximidades de vemos que a concavidade da função é para cima, o que indica uma aceleração positiva. No entanto, se traçarmos uma reta tangente em notamos que a derivada é negativa, o que implica em . Sendo assim, podemos concluir que a velocidade é negativa em !