Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.6 - Ex. 21
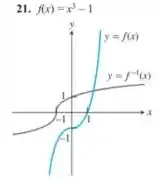
Cada um dos exercícios 19-24 apresenta a fórmula de uma função e mostra os gráficos de e . Determine uma fórmula para em cada caso.
Passo 1
Para fazermos a inversa da função, assim como discutido na seção 6 do George, devemos escrever uma função , isto é, isolar a variável na função (supondo que seja a variável) e em seguida trocarmos as variáveis para escrevermos a inversa na forma convencional, que é , tranquilo? Se liga!
Passo 2
Como a nossa função é , escrevendo , temos:
Passo 3
Agora que encontramos a função , só devemos inverter as variáveis para escrevermos a função na forma convencional, que é . Sendo assim, a inversa da será:
Resposta
Exercícios de Livros Relacionados
Quais funções representadas graficamente nos Exercícios 1-6 são injetoras e quais não são?
Quais funções representadas graficamente nos Exercícios 1-6 são injetoras e quais não são?
Quais funções representadas graficamente nos Exercícios 1-6 são injetoras e quais não são?
Nos Exercícios 7-10, identifique, a partir de seu gráfico, se a função é injetora.7. f x = 3 - x , x0 3 , x ≥ 0
Nos Exercícios 7-10, identifique, a partir de seu gráfico, se a função é injetora.10. f x = 2 - x ² , x ≤ 1 x ² , x1 ² ²