Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.6 - Ex. 4
Quais funções representadas graficamente nos Exercícios 1-6 são injetoras e quais não são?
Passo 1
Para resolvermos os exercícios do 1-6, devemos lembrar da definição de função injetora, tudo bem?
Uma função é injetora em um domínio se , sempre que em .
Há duas formas de provar se uma função é injetora ou não. A primeira é pelo gráfico. Se traçarmos uma reta paralela ao eixo (imaginária) e o gráfico da função tocar a reta 2 vezes, isso implica que a função não é injetora; mas caso toque apenas 1 vez, isso implica que a função é injetora.
A segunda maneira é usando a definição e atribuindo valores a , ou seja, se aplicarmos 2 valores distintos de na função e der o mesmo valor de , isso implica que a função não é injetora.
Passo 2
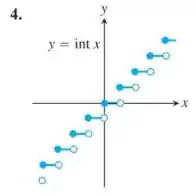
Nessa questão nem precisamos plotar gráficos e nem nada para resolve-la! Percebe-se que a função se trata de infinitas retas. Dessa forma, se traçarmos retas em cima de retas é IMPOSSÍVEL que a função só toque a reta em um único ponto, não é mesmo? Sendo assim, a função não é injetora!
Resposta
A função não é injetora.