Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 4.2 - Ex. 29

Em cada um dos problemas de 29 a 36, encontre a solução do problema de valor inicial dado e faça seu gráfico. Como a solução se comporta quando t → ∞ ?

29. y ' ' ' + y ' = 0 ;           y 0 = 0 ,         y ' 0 = 1 ,           y ' ' 0 = 2

Passo 1

A primeira coisa que temos que fazer aqui é resolver essa equação aqui:

r 3 + r = 0   →

Que é a equação característica da EDO, saca?

Beleza! Então colocando o r em evidência...

r r 2 + 1 = 0  

Dessa equação já dá para ver quem vai ser a primeira raiz da equação característica, neh?

r 1 = 0

Para encontrar as outras raízes, devemos fazer com que o outro termo seja zero...

r 2 + 1 = 0     →

r 2 = - 1   →

r = ± - 1

Como - 1 é a unidade complexa i ... As demais raízes dessa equação serão...

r 2 = i       e           r 3 = - i

Passo 2

Beleza, então podemos montar a solução dessa EDO de acordo com os valores de r . Vamos nessa?

Vamos começar montando as soluções fundamentais para dada r :

  • Para r 1 = 0 como ele é real...

    • y 1 = e r 1 t = e 0 = 1

  • Para r 2 = i , por complexa do tipo a + b i ...

    • y 2 = e a t sin ⁡ b t = e 0 sin ⁡ t

  • Para r 3 = - i , por ser imaginário também e conjugado do anterior...

y 3 = e a t cos ⁡ b t = e 0 cos ⁡ t

A solução geral então pode ser dada por...

y = c 1 y 1 + c 2 y 2 + c 3 y 3   →

y = c 1 + c 2 sin ⁡ t + c 3 cos ⁡ t

Onde c ’s representam as constantes que dependem das condições iniciais então vamos calcular!

Passo 3

Como sabemos, as condições inicias são essas daqui: y 0 = 0 ,   y ' 0 = 1 ,   y ' ' 0 = 2 .

Substituindo a primeira condição...

y 0 = c 1 + c 2 sin ⁡ 0 + c 3 cos ⁡ 0   →

0 = c 1 + c 3  

Beleza, então antes de analisar a condição 2, temos que derivar a função...

y = c 1 + c 2 sin ⁡ t + c 3 cos ⁡ t   →

y ' = c 2 cos ⁡ t - c 3 sin ⁡ t

Substituindo a segunda condição...

y ' 0 = c 2 cos ⁡ 0 - c 3 sin ⁡ 0   →

1 = c 2

Para a última condição, calculemos agora a segunda derivada...

y ' ' = - c 2 sin ⁡ t - c 3 cos ⁡ t

y ' ' 0 = - c 2 sin ⁡ 0 - c 3 cos ⁡ 0   →

2 = - c 3   →

c 3 = - 2

Então...

0 = c 1 + c 3   →

c 1 = 2

Então a solução do nosso PVI é...

y = c 1 + c 2 sin ⁡ t + c 3 cos ⁡ t   →

y = 2 + sin ⁡ t - 2 cos ⁡ t

Passo 4

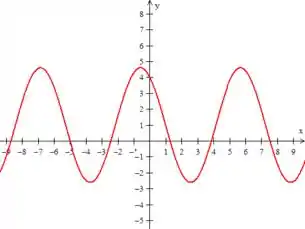
Podemos desenhar essa função y usando algum programinha de plotagem de função, onde vamos ganhar...

Veja que a solução tem um comportamento senoidal. Quando t for para o infinito, como temos apenas seno e cosseno na resposta...

y = 2 + sin ⁡ t - 2 cos ⁡ t

E nenhuma exponencial envolvida, a resposta vai continuar tendo o mesmo comportamento senoidal!

Resposta

y = 2 + sin ⁡ t - 2 cos ⁡ t

A função terá um comportamento senoidal para qualquer t :

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos problemas 1-36, encontre a solução geral para a equação diferencial dada. y ' ' + 9 y = 0
Nos problemas 1-36, encontre a solução geral para a equação diferencial dada. 4 y ' ' + y ' = 0
Nos problemas 1-36, encontre a solução geral para a equação diferencial dada. d ² y d x ² - 10 d y d x + 25 y = 0 ² ²
Nos problemas 1-36, encontre a solução geral para a equação diferencial dada. d ² y d x ² + 8 d y d x + 16 y = 0 ² ²
Nos problemas 1-36, encontre a solução geral para a equação diferencial dada. 12 y ' ' - 5 y ' - 2 y = 0