Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.2 - Ex. 25

Em cada um dos problemas de23 a 26,use a fórmula de Euler modificada do Problema 22 com h   =   0,05 para calcular valores aproximados da solução do problema de valor inicial dado em t   =   0,1 ;   0,2 ;   0,3   e   0,4 . Compare os resultados com os obtidos nos Problemas de 1 a 4 .

25. y ' = 2 y - 3 t ,     y 0 = 1

Passo 1

Bora lá pra mais um probleminha sobre métodos numéricos.

Olha só! A fórmula de E u l e r modificada para a equaçãozinha do nosso problema tem a seguinte cara...

y n + 1 = y n + h 2 y n - 3 t n - 3 2 h + h 2 y n - 3 t n

Mexendo um pouco nela, ficamos com...

y n + 1 = y n + h 2 y n - 3 t n + h 2 2 4 y n - 6 t n - 3

Só que nós sabemos que...

t n = t 0 + n h

Com...

t 0 = 0

Desse modo, a nossa fórmula de y n + 1 vai ficar...

y n + 1 = y n + h 2 y n - 3 t n + h 2 2 4 y n - 6 t n - 3

y n + 1 = y n + h 2 y n - 3 n h + h 2 2 4 y n - 6 n h - 3

Pronto! O primeiro passo já foi traçado. Vamos agora, partir pra resolução computacional...

Passo 2

Para isso, vamos usar a seguinte estrutura abaixo em forma de algoritmo a fim de fazer o nosso código...

P a s s o   1 : D e f i n i r   a   f u n ç ã o   y n + 1  

P a s s o   2 : D e f i n i r   o   t a m a n h o   d o   p a s s o   h   e   o   n ú m e r o   d e   p a s s o s   n    

P a s s o   3 : P a r a   i   d e   1   a t é   u m   t a m a n h o   d e   0 . 4 h   f a ç a  

P a s s o   4 :  

y n + 1 = y n + h 2 y n - 3 n h + h 2 2 4 y n - 6 n h - 3

i = i + 1  

n = n + 1  

P a s s o   5 : E s c r e v a l   y n + 1

P a s s o   6 : F i m

Passo 3

Desse modo, utilizando uma linguagem de programação qualquer, C ou P y t h o n , é possível determinar o que a gente quer. No caso, bora usar a C ...

Usando o seguinte código abaixo, feito com todo carinho do mundo...

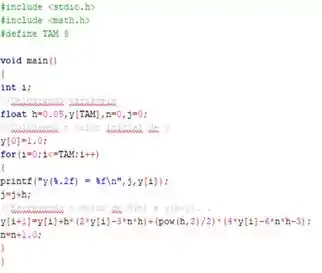
E compilando ele, num total de iterações ( T A M ) , igual à...

T A M = 0.4 h

T A M = 0.4 0.05 = 8

Chegamos até o demonstrado na imagem adiante...

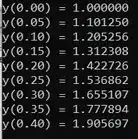
E assim, obtemos a seguinte tabela:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos problemas16 e 17, estimeo erro de truncamentolocal para o método de Euler em termos da solução y ' = ϕ ( t ) . Obtenha uma cota para e n + 1 em termos de t e de ϕ ( t ) que seja válida no interval
Nos problemas16 e 17, estimeo erro de truncamentolocal para o método de Euler em termos da solução y ' = ϕ ( t ) . Obtenha uma cota para e n + 1 em termos de t e de ϕ ( t ) que seja válida no interval
Em cada um dos problemas de 1 a 6, encontre valores aproximados da soluçãodo problema de valor inicial dado em t = 0,1; 0,2; 0,3 e 0,4. Compare osresultados comos obtidos pelométodo de Euler e pelomét
Em cada um dos problemas de 1 a 6, encontre valores aproximados da soluçãodo problema de valor inicial dado em t = 0,1; 0,2; 0,3 e 0,4. Compare osresultados comos obtidos pelométodo de Euler e pelomét
Em cada um dos problemas de 1 a 6, encontre valores aproximados da soluçãodo problema de valor inicial dado em t = 0,1; 0,2; 0,3 e 0,4. Compare osresultados comos obtidos pelométodo de Euler e pelomét