Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 3.3 - Ex. 3
Em cada um dos problemas de 1 a 6, use a fórmula de Euler para escrever a expressão dada na forma .
Passo 1
Para o nosso probloma, apenas lembre que . Agora vamos começar nosso problema realizando manipulações matemáticas.
Passo 2
Olhando para o Passo 1, temos que
Lembrando do arco trigonométrico
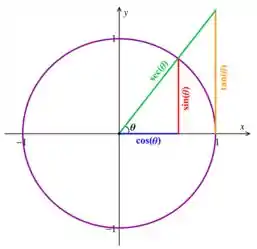
Podemos perceber que em temos que e = 0
Assim temos que
Um problema simples, se lembrarmos de algumas coisinhas, hahaha.
Resposta
Exercícios de Livros Relacionados
Em cada um dos problemas de 7 a 16, encontre a solução geral da equação diferencial dada. y ' ' - 2 y ' + 2 y = 0
Em cada um dos problemas de 17 a 22, encontre a solução do problema de valor inicial. Esboçe o gráfico da solução e descreva seu comportamento para valores cada vez maiores de t . y ' ' + y = 0 ,y π /
Em cada um dos problemas de 17 a 22, encontre a solução do problema de valor inicial. Esboçe o gráfico da solução e descreva seu comportamento para valores cada vez maiores de t . y ' ' + 4 y = 0 ,y 0
Em cada um dos problemas de 7 a 16, encontre a solução geral da equação diferencial dada. y ' ' + 2 y ' + 1,25 y = 0
Em cada um dos problemas de 7 a 16, encontre a solução geral da equação diferencial dada. y ' ' + 4 y ' + 6,25 y = 0