Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 7.9 - Ex. 16

Calcular a área sob a curva y = (1)/(2 + cos x) e y = (1)/(2 - cos x) , de x = - (pi)/(2) a x = (pi)/(2) .

Passo 1

A área pedida é a da figura abaixo:

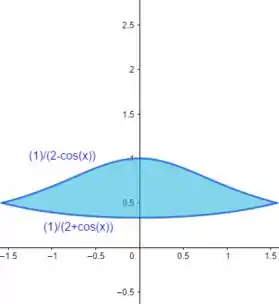
Como a gente pode ver, a função que está por cima é a y = (1)/(2 - cos x) . Então a gente encontra a área fazendo:

A = int_(- (pi)/(2))^((pi)/(2)) (1)/(2 - cos x) - (1)/(2 + cos x) d x

Vamos lá, aqui a gente tem uma função racional de seno e cosseno.

O próprio livro dá o macete pra resolver esse tipo de integral. Nesse caso aqui vai ficar

t = t g (x)/(2)

E com isso a gente tem que:

c o s x = (1 - t^2)/(1 + t^2) e d x = (2 d t)/(1 + t^2)

Passo 2

Vamos separar em duas integrais pra ficar mais fácil:

A = int_(- (pi)/(2))^((pi)/(2)) (1)/(2 - cos x) d x - int_(- (pi)/(2))^((pi)/(2)) (1)/(2 + cos x) d x

A gente pode resolver com integral indefinida e trocar depois pra usar os intervalos de integração.

Vamos resolver então assim:

int (1)/(2 - cos x) d x - int (1)/(2 + cos x) d x

Agora a gente substitui...

int (1)/(2 - (1 - t^2)/(1 + t^2)) * (2 d t)/(1 + t^2) - int (1)/(2 + (1 - t^2)/(1 + t^2)) * (2 d t)/(1 + t^2)

int ((2 d t)/(1 + t^2))/((2 + 2 t^2 - 1 + t^2)/(1 + t^2)) - int ((2 d t)/(1 + t^2))/((2 + 2 t^2 + 1 - t^2)/(1 + t^2))

Passo 3

Vamos simplificar agora:

int (2 d t)/((3 t^2 + 1)) - int (2 d t)/(t^2 + 3)

Aí a gente pode fazer:

(2)/(3) int (d t)/(t^2 + (1)/(3)) - 2 int (d t)/(t^2 + 3)

Aí agora a gente integra:

= (2)/(sqrt(3)) a r c t g sqrt(3) - (2)/(sqrt(3)) a r c t g (t)/(sqrt(3)) + C

Vamos voltar pra nossa variável inicial agora:

= (2)/(sqrt(3)) a r c t g (sqrt(3) t g ((x)/(2))) - (2)/(sqrt(3)) a r c t g ((1)/(sqrt(3)) t g ((x)/(2))) + C

Passo 4

Beleza, agora pra achar a área agora a gente aplica os intervalos de integração:

A = [(2)/(sqrt(3)) a r c t g (sqrt(3) t g ((x)/(2))) - (2)/(sqrt(3)) a r c t g ((1)/(sqrt(3)) t g ((x)/(2)))]_(- (pi)/(2))^((pi)/(2))

A = (2)/(sqrt(3)) a r c t g sqrt(3) - (2)/(sqrt(3)) a r c t g (1)/(sqrt(3)) - (2)/(sqrt(3)) a r c t g (- sqrt(3)) + (2)/(sqrt(3)) a r c t g - (1)/(sqrt(3))

A = (2)/(sqrt(3)) * (pi)/(3) - (2)/(sqrt(3)) * (pi)/(6) + (2)/(sqrt(3)) * (pi)/(3) - (2)/(sqrt(3)) * (pi)/(6)

A = (2 pi)/(3 sqrt(3)) = (2 sqrt(3))/(9) u . a

Prontinho! Essa é a área pedida😉

Resposta

A = (2 sqrt(3))/(9) u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5-18. Calcule a integral definida de duas formas: primeiro com uma substituição u na integral definida e, depois, com uma substituição u na integral indefinida.16. ∫ 0 ln ⁡ 5 e x 3 - 4 e x d x
31-50. Calcule as integrais por qualquer método.45. ∫ 0 e d x 2 x + e
31-50. Calcule as integrais por qualquer método.44. ∫ - 1 4 x 5 + x d x
31-50. Calcule as integrais por qualquer método.40. ∫ π 2 4 π 2 1 x . s e nx d x
31-50. Calcule as integrais por qualquer método.39. ∫ 0 π 5 x . cos ⁡ x 2 d x