Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 6.13 - Ex. 12

Encontrar a área da região limitada pelas curvas dadas.

y = ln ⁡ x ,   x = 1   e   y = 4

Passo 1

A região é essa:

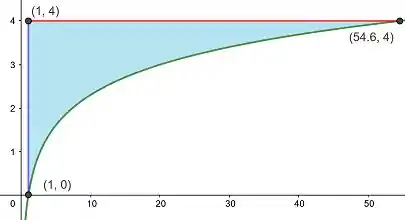
Passo 2

Vamos ver a interseção da curva y = ln ⁡ x com a curva y = 4 (a que tá na figura é um valor aproximado, vamos calcular o exato).

ln ⁡ x = 4

x = e 4

Beleza, então a interseção das duas ocorre em x = e 4 .

A nossa região de integração então vai de 1 a e 4 .

Passo 3

A área então é dada por:

A = ∫ 1 e 4 4 - ln ⁡ x   d x

Aí integrando a gente tem:

A = 4 x - x ln ⁡ x + x 1 e 4

A = 4 e 4 - e 4 ln ⁡ e 4 + e 4 - 4 - ln ⁡ 1 + 1

A = 4 e 4 - e 4 4 + e 4 - 4 - 1

A =   e 4 - 5   u . a

Prontinho! Essa é a área da região😉

Resposta

A =   e 4 - 5   u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

7-18 Esboce a região englobada pelas curvas e encontra a área16. y = 1 1 - x 2 , y = 2
7-18 Esboce a região englobada pelas curvas e encontra a área18. y = x , y = 4 x , y = - x + 2
Encontre a área da região sombreada:
Encontre a área da região sombreada integrando em relação a x:
Encontre a área da região sombreada: