Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.Exercícios práticos - Ex. 74
Complete os quadrados para identificar as seções cônicas nos Exercícios 69-76. Encontre seus focos, vértices, centros e assíntotas (conforme apropriado). Se a curva for uma parábola, encontre também sua diretriz.
Passo 1
Olá galerinha, espero que estejam bem e ansiosos para resolver este exercício comigo! Vamos lá.
As seções cônicas resultam da intersecção de um cone plano, como mostrado na Figura:
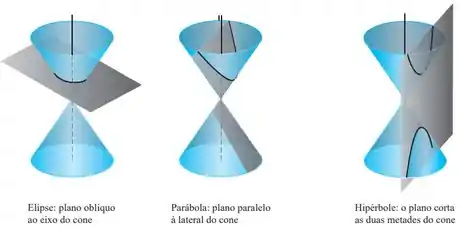
Equações de forma padrão para elipses centradas na origem:
- Distância entre o centro e foco:
- Focos:
- Vértices:
- Se concavidade para baixo;
- Se concavidade para cima.
- Distância entre o centro e foco:
- Focos:
- Vértices:
- Assíntotas: ou
- Elipse:
- Parábola:
- Hipérbole:
Uma equação da parábola com foco e diretriz é:
Se considerarmos que , então a equação torna-se:
Equações de forma padrão para hipérbole centradas na origem:
As equações cônicas descritas anteriormente têm todas focos no eixo e, centro ou vértice em . Quando temos um centro genérico em e focos na reta são:
Passo 2
Sabendo disso, vamos para o nosso exercício, onde temos a seguinte equação:
Primeiramente iremos agrupar os termos em e os termos em :
Completando o quadrado:
Vemos que se trata de uma elipse com , e:
Porém, como , iremos calcular o vértice e o foco em relação ao eixo .
Passo 3
Podemos perceber que os valores de e estão deslocados, logo o centro será:
Sendo assim .
Para o vértice temos o seguinte:
Logo:
E por fim, temos o foco:
Resposta
Elipse: , , , e .