Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.1 - Ex. 32
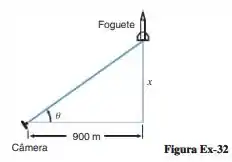
Conforme mostra a figura abaixo, uma câmara é montada em um ponto a 900 m da base de lançamento de um foguete. Quando lançado, o foguete sobe verticalmente, e o ângulo de elevação da câmera é constantemente ajustado para seguir a base do foguete.
(a) Expresse a altura x como uma função do ângulo θ de elevação.
(b) Determine o domínio da função em (a).
(c) Gere o gráfico da função em (a) e use-o para estimar a altura do foguete, quando seu ângulo de elevação for π/4 ≈ 0,7854 radianos. Compare essa estimativa com a altura exata.
Passo 1
(a) Bom, vamos usar a própria figura dada pelo problema para achar a relação entre e .
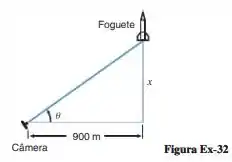
Pelo triângulo formado, vamos usar a relação da tangente de :
Como expressar em função de , vamos isolar ele na equação:
Passo 2
(b) O domínio representa os valores de .
Então, como definimos a função por um triângulo retângulo, deve ser menor que . E essa será a nossa única restrição haha:
Passo 3
(c) Plotando o gráfico:
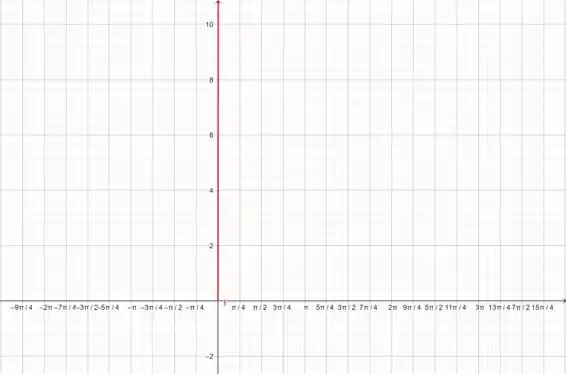
Então, bem ruim de plotar né kkk é quase uma reta. E o pior é que não vi um gráfico mais visível que esse, maaasss podemos chutar um valor absurdo de para , confia em mim.
E não é à toa, o valor real seria:
Como :
Resposta
(a)
(b)
(c)