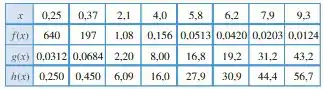
A tabela abaixo dá valores aproximados de três funções: uma da forma k x 2 , outra da forma k x - 3 e a terceira da forma k x 3 2 . Identifique cada uma e dê uma estimativa de k em cada caso.

f x = k x - 3 g x = k x 2 h x = k x 3 2

Enunciado

Bom, então temos 3 funções:

Vamos arrumar elas:

acaba sendo diretamente proporcional ao .

é inversamente proporcional ao .

é diretamente proporcional ao .

Então, vamos identificar a proporcionalidade das funções na tabela com e ver em qual desses casos elas se encaixam.

Olhando para na tabela:

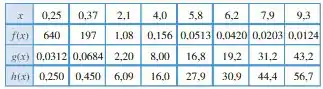
A gente pode ver que, conforme aumenta, diminui, ou seja, eles são inversamente proporcionais! Dessa forma, se encaixa no segundo estilo de função:

Sobraram duas opções para gente: , que é diretamente proporcional a , e , que é diretamente proporcional .

Como , já que , esperamos que a função relacionada ao cresça mais rápido que a relacionada ao , certo?

Olhando para a tabela, vemos que saiu de para . O que nos dá uma proporção de:

Já saiu de para :

Como a razão entre o último número e o primeiro de foi maior, podemos dizer que ele cresceu mais que . Dessa forma, ele será relacionado ao :