Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.4 - Ex. 16

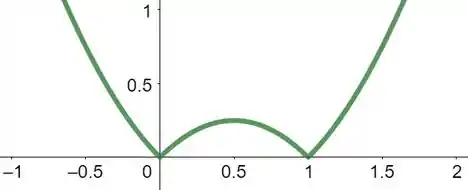
Determine uma janela de visualização apropriada para a função dada e a utilize para exibir o gráfico da função:

Passo 1

Esta é uma questão que necessita de recursos tecnológicos para ser resolvida. Sendo assim, utilizaremos de softwares para obtermos o gráfico da função. Entretanto, antes de colocarmos a “mão na massa”, é necessário discutir o que é uma janela de visualização apropriada. Com estas palavras, a questão pede que, dentro de uma janela, todas as propriedades de uma função estejam nelas, isto é: mudanças de concavidade ou de crescimento/decrescimento; se existe algum máximo/mínimo local; comportamento quando ela vai para o valor de vai para o infinito; etc.

Vamos exemplificar essa teoria, e para isto tome a função periódica . Basta obtermos uma janela com o eixo variando entre e o eixo variando entre que conseguimos esboçar todo o comportamento da nossa função.

Sendo assim, a nossa análise inicial consistirá em obter duas janelas de visualização: uma grande (amplitude da variação de alta) e uma pequena. A partir destas duas janelas, será discutido as propriedades da função e ajustes serão feitos na janela para assim obtermos uma janela apropriada e o gráfico final da função.

Passo 2

Vejamos então duas janelas iniciais:

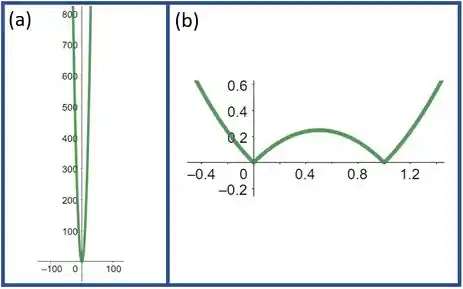
O gráfico da esquerda (a) e o da direita (b) são as de janela grande e pequena respectivamente. Como a função é modular, é esperado que haja uma simetria em torno de , para um valor de . Observando a de janela grande é possível observar a simetria da função, sendo que, à medida que aumenta, também aumenta. Além disto, confirmamos visualmente que .

Já ao observarmos o gráfico (b), pode-se visualizar a simetria aproximadamente em torno de . Além disto, visualizamos um ponto de máximo local em (antes dele a função cresce e depois ela decresce) e pontos de mínimo local em e (antes dele a função decresce e depois dele ela cresce).

Sendo assim, a janela final deve conter as propriedades discutidas no gráfico (a) e (b).

Passo 3

Vamos agora obter um novo gráfico e observar se é possível visualizar tudo que foi discutido anteriormente. Portanto, temos:

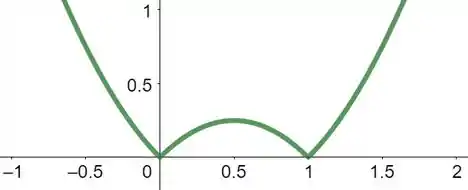
O gráfico assim, cuja janela é por apresenta todas as propriedades discutidas no passo 2. Logo, é uma janela de visualização apropriada para a nossa função.