Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.5 - Ex. 5

Considere outro modelo caçador competitivo definido por

d x d t = a ⋅ 1 - x k 1 ⋅ x - b x y ,

d y d t = m ⋅ 1 - y k 2 ⋅ y - n x y

onde x e y   representam as populações de trutas e percas, respectivamente.

  1. Que suposições são feitas implicitamente sobre o crescimento das trutas e das percas na ausência de concorrência?
  2. Interprete as constantes a ,   b ,   m ,   n , k 1 e k 2 em termos do problema físico.
  3. Faça uma análise gráfica:
  1. Determine os níveis de equilíbrio possíveis.
  2. Determine se a coexistência é possível.
  3. Escolha vários pontos de partida típicos e esboce as trajetórias típicas no plano de fase.
  4. Interprete os resultados previstos por sua análise gráfica em termos das constantes a ,   b ,   m ,   n ,   k 1   e   k 2 .

Nota: ao chegar à parte ( i i i ) , você perceberá que existem cinco casos. Será necessário analisar todos eles.

Passo 1

O crescimento logístico na ausência de concorrência e a interação simples das espécies leva em consideração que o crescimento domina sobre a competição quando uma população é pequena, por isso fica bastante difícil levar ambas as espécies à extinção.

Passo 2

As variáveis do problema podem ser interpretadas da seguinte forma:

a = Crescimento per capita da truta

b = Intensidade da competição com a truta

m = Crescimento per capita da perca

n = Intensidade da competição com a perca

k 1 = Capacidade de carga ambiental da truta

k 2 =   Capacidade de carga ambiental da perca

Passo 3

Vamos encontrar, primeiramente, os pontos de equilíbrio que são os casos onde temos as derivadas iguais a 0. Dessa forma,

a ⋅ 1 - x k 1 ⋅ x - b x y = 0

x ⋅ a ⋅ 1 - x k 1 - b y = 0 → x = 0   o u   a ⋅ 1 - x k 1 - b y = 0  

a ⋅ 1 - x k 1 - b y = 0 → y = a b - a x b k 1

Para a outra equação

m ⋅ 1 - y k 2 ⋅ y - n x y = 0 → y ⋅ m ⋅ 1 - y k 2 - n x = 0

→ y = 0   o u   m ⋅ 1 - y k 2 - n x = 0 → x = m n - m y n k 2

Dessa forma, como foi previsto no enunciado temos 5 casos para verificar

1º caso: a b > k 2   e m n > k 1 garante um ponto de equilíbrio no primeiro quadrante

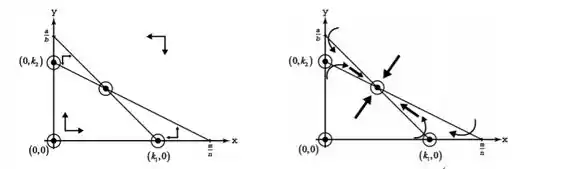
Vamos ter 4 pontos de equilíbrio: 0,0 ,   k 1 , 0 ,   0 , k 2   e   a m k 1 - b m k 1 k 2 a m - b n k 1 k 2 , a m k 2 - a n k 1 k 2 a m - b n k 1 k 2 onde apenas o ponto de interseção das curvas será equilíbrio estável, a possibilidade de coexistência é prevista nesse modelo.

2º caso: a b > k 2   e m n < k 1

0 , k 2 : equilíbrio instável

k 1 , 0 : equilíbrio estável (aqui as trutas ganham)

0,0 : equilíbrio instável

Não é possível a coexistência

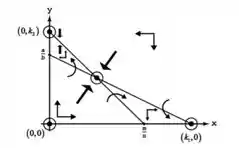
3º caso: a b < k 2   e m n > k 1

0 , k 2 : equilíbrio estável (aqui as percas ganham)

k 1 , 0 : equilíbrio instável

0,0 : equilíbrio instável

Não é possível a coexistência

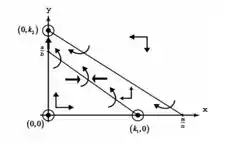
4º caso: a b < k 2   e m n < k 1

0 , k 2 : equilíbrio estável

k 1 , 0 : equilíbrio estável

0,0 : equilíbrio instável

a m k 1 - b m k 1 k 2 a m - b n k 1 k 2 , a m k 2 - a n k 1 k 2 a m - b n k 1 k 2 : equilíbrio instável

Trutas ou percas podem ganhar

É possível a coexistência, mas não é prevista

5º caso: a b = k 2   e a b k 1 = n k 2 m as curvas coincidem

0 , k 2 : equilíbrio estável

k 1 , 0 : equilíbrio estável

0,0 : equilíbrio instável

O segmento que liga os pontos de estabilidade são também estáveis e a coexistência é um resultado provável.

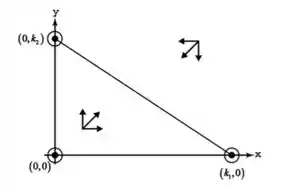
Todos os pontos presentes nessa reta que liga os 2 pontos são pontos de descanso.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula move-se ao longo de uma linha reta, em t segundos, s é a distância orientada da partícula até a origem, v m/s é a sua velocidade e a m/s² é a sua aceleração. (24) a = 17 ; v = 0es = 0 q
Uma partícula move-se ao longo de uma linha reta, em t segundos, s é a distância orientada da partícula até a origem, v m/s é a sua velocidade e a m/s² é a sua aceleração. (26) a = 3 t - t 2 ; v = 7 6
Uma partícula move-se ao longo de uma linha reta, em t segundos, s é a distância orientada da partícula até a origem, v m/s é a sua velocidade e a m/s² é a sua aceleração. (27) a = 5 s + 2 ; v = 4es =
Uma partícula move-se ao longo de uma linha reta, em t segundos, s é a distância orientada da partícula até a origem, v m/s é a sua velocidade e a m/s² é a sua aceleração. (27) a = - 4 2 c o s ⁡ ( 2 t
Uma partícula move-se ao longo de uma linha reta, em t segundos, s é a distância orientada da partícula até a origem, v m/s é a sua velocidade e a m/s² é a sua aceleração. (27) a = 2 s + 1 ; v = 2es =