Exercícios de Modelagens com Equação Separável - Lista de Exercícios Resolvida
Questão 1
Considere a lei de resfriamento de Newton, , em que a temperatura do meio ambiente varia com o tempo. Suponha que a temperatura inicial de um corpo seja e que a temperatura inicial do meio ambiente seja e , em que seja uma constante.
- Encontre a temperatura do corpo em qualquer instante .
- Qual é o valor limite da temperatura quando ?
- Qual o valor limite de quando ?
Questão 2
A reta tangente ao gráfico de , no ponto , intercepta o eixo no ponto de ordenada . Determine sabendo que .
Ver solução completaQuestão 3
Dois compostos químicos e são combinados para formar um terceiro composto . A taxa ou velocidade da reação é proporcional à quantidade instantânea de e não convertida em . Inicialmente há 40 gramas de e 50 gramas de , e para cada grama de 2 gramas de são usados. É observado que 10 gramas de são formados em 5 minutos. Qual é a quantidade remanescente de e depois de um longo período de tempo?
Ver solução completaQuestão 4
Um trenó foguete com velocidade inicial de 150 milhas/h (cerca de 241km/h) tem sua velocidade diminuída por um canal de água. Suponha que durante o processo de freagem a aceleração é dada por , onde é a velocidade e é uma constante.
- Use a relação para escrever a equação de movimento em função de e de .
- Se é necessária uma distância de 2000 pés (cerca de 609.6m) para o trenó atingir a velocidade de 15 milhas/h, determine o valor de
- Encontre o tempo necessário para o trenó atingir a velocidade de 15 milhas/h.
Questão 5
Suponha que um foguete é projetado da superfície da Terra diretamente para cima com velocidade inicial , onde é o raio da Terra. Despreze a resistência do ar.
- Encontre uma fórmula para a velocidade em função da distância à superfície da Terra.
- Encontre o tempo necessário para o foguete percorrer 240.000 milhas(a distância aproximada da Terra à Lua). Suponha que milhas
Questão 6
Suponha que no instante , a metade de uma população de coelhos é infectada por um vírus que começa crescendo com uma taxa de coelhos por dia. Assumindo que a taxa com que o vírus se espalha é proporcional à quantidade de coelhos infectados vezes a quantidade de coelhos não infectados, determine o tempo que levará para que o vírus se espalhe por da população.
Ver solução completaQuestão 7
Uma doença rara se espalha em uma aldeia indígena de habitantes, e a taxa de variação das pessoas infectadas é proporcional ao quadrado da quantidade de pessoas infectadas vezes a quantidade de pessoas não infectadas. Inicialmente, há apenas uma pessoa infectada, porém após um dia, pessoas estão infectadas. Qual alternativa é o modelo matemático apropriado para estudar a evolução dessa doença?
(a)
(b)
(c)
(d) Nenhuma das outras opções
(e)
Ver solução completaQuestão 8
Considere uma espécie cuja população no instante satisfaz a equação diferencial seguinte:
- Se a população inicial , a população tenderá a longo prazo um valor de equilíbrio? Em caso positivo, qual?
- Se a população inicial , a população tenderá a longo prazo um valor de equilíbrio? Em caso positivo, qual?
Questão 9
Uma colônia de bactérias aumenta sua população a uma taxa proporcional a quantidade de bactérias presente em cada instante de tempo, com população inicial segundo a equação diferencial:
- Encontre a solução geral da equação diferencial
- Se em horas a população triplica, em quanto tempo ela será vezes o valor inicial.
Questão 10
Um tanque com capacidade para litros está qcheio de água pura. Água salgada contendo de sal por litro entra no tanque a uma taxa de . A solução é agitada e retirada do tanque a mesma taxa. Seja a quantidade de sal no tanque a cada minuto.
Escreva uma equação diferencial que represente a taxa de variação da quantidade de sal no tanque. A taxa de variação de quantidade de sal no tanque é a diferença entre a taxa que entra e a taxa que sai.
Obtenha a solução geral desta equação.
Obtenha a quantidade de sal no tanque após hora.
Calcule
Ver solução completaQuestão 11
Uma tigela de sopa sai do aparelho de micro-ondas a e é levada para uma sala onde a temperatura é de . A lei de resfriamento de Newton afirma que a taxa de resfriamento é proporcional à diferença de temperatura entre o objeto e sua vizinhança. Sabemos também que esta sopa esfria a uma taxa de por minuto quando sua temperatura é de :
Escreva a equação diferencial que expressa a lei de resfriamento de Newton nesta situação particular.
Resolva a equação diferencial e determine a temperatura da sopa meia hora após ter chegado à sala.
Esboce um gráfico que represente a temperatura da sopa a partir do momento que chegou a sala.
Ver solução completaQuestão 12
Determine a função cujo gráfico contém o ponto tal que para todo do gráfico de a área da região seja o dobro da área da região , conforme a figura ao lado.
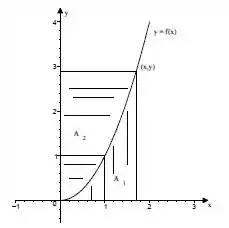
Questão 13
Um material radioativo se desintegra a uma taxa proporcional à quantidade presente em cada instante. Supondo que a quantidade inicial de material que seja e que anos depois já tenha desintegrado do material inicial, determine sua meia-vida.
Ver solução completaQuestão 14
Suponha que uma gota d’água esférica evapore a taxa proporcional à área de sua superfície. Se o raio mede originalmente mm e h depois foi reduzido a mm, encontre a expressão do raio em função do tempo.
Ver solução completaQuestão 16
A população mundial era de bilhões em e de bilhões em .
Encontre um modelo exponencial para estes dados.
Use o modelo encontrado para prever a população no ano de ( anos depois).
De acordo com o modelo encontrado, quando a população excederá bilhões?
Ver solução completaQuestão 17
Uma colônia de bactérias aumenta sua população a uma taxa proporcional à quantidade de bactérias presente em cada instante de tempo. Se em quatro horas a população triplica, em quanto tempo ela será vezes a quantidade inicial?
Ver solução completaQuestão 18
Sabemos que, se uma solução particular da equação ordinária de ordem:
Então é a solução geral, onde satisfaz a equação linear:
Obtenha a partir de , supondo que satisfaz .
Obtenha a solução geral da equação logística
Sabendo que é uma solução particular. Use o resultado acima!
Determine os pontos de equilíbrio desta equação logística, e os classifique quanto a estabilidade.
Ver solução completaQuestão 19
Teste 11: Considere a EDO
Analise as seguintes afirmações:
- A função é uma possível solução da EDO tal que .
- Se é solução da EDO tal que , então para .
- Sua solução geral é .
São verdadeiras:
- Apenas .
- Apenas .
- Todas.
- Apenas e .
- Apenas .
Questão 20
Um investidor aplica na bolsa de valores determinada quantia que triplica em 30 meses. Em quanto tempo essa quantia estará quadruplicada, supondo-se que a quantidade aplicada aumenta a uma taxa proporcional ao investimento feito a cada instante?
Dica: Assuma que .
Ver solução completaQuestão 21
Um reservatório contém litro de água salgada com kg de sal dissolvido. Água salgada com kg de sal por litro de água entra no tanque a uma taxa de litros por minuto. Solução é mantida completamente misturada e escoa do tanque a uma taxa de litros por minuto.
- Escreva uma equação diferencial que represente a taxa de variação da quantidade de sal no tanque a medida que o tempo passa.
- Resolva a equação diferencial e determine a quantidade de sal minutos após iniciada a experiência.
- Quanto sal há no tanque após horas.
- Calcule o limite da quantidade de sal no tanque quando .
Questão 22
Considere o modelo logístico de dinâmica populacional:
onde , são constantes positivas e .
- Obtenha soluções para o problema de valor inicial ;
- Esboce o gráfico do espaço de fase para o modelo, e determine os pontos de equilíbrio tal que , e classifique estes pontos como estáveis quando ou instáveis quando
Questão 23
Resolva a equação diferencial abaixo por separação de variáveis.
( )
( )
( )
( )
( )
Ver solução completaQuestão 24
Uma colônia de microrganismos aumenta sua população a uma taxa proporcional à quantidade de indivíduos presentes em cada instante de tempo, com população inicial , segundo a equação
Se em horas a população triplica, em quanto tempo ela será 27 vezes a população inicial?
Ver solução completaQuestão 26
4. Coloca-se uma barra de metal à temperatura de em um quarto com temperatura constante de . Se, após 20 min, a temperatura da barra é de , determine:
b) A temperatura da barra após 10 min.
Ver solução completaQuestão 27
5. Coloca-se um corpo com temperatura desconhecida em um quarto mantido à temperatura constante de Se após 10 min a temperatura do corpo é de e após 20 min é de , determine a temperatura inicial.
Ver solução completaQuestão 28
Inicialmente, havia miligramas de uma substância radioativa presente. Após horas a massa diminuiu . Se a taxa de decrescimento é proporcional à quantidade de substância presente em qualquer tempo, encontre a quantidade remanescente após horas.
Ver solução completaQuestão 29
7. Determine uma família de curva , , , que satisfazem a seguinte propriedade: no intervalo , a ordenada é proporcional à área determinada pela curva, os eixos coordenados e a reta vertical que contém a abcissa .
Ver solução completaQuestão 30
8. Certa substância radioativa decresce a uma taxa proporcional à quantidade presente. Se observa que após 1 hora, houve uma redução de 10% da quantidade inicial. Determine a meia-vida da substância (meia-vida de uma substância radioativa é o tempo que a substância leva para que sua massa decaia à metade da quantidade original).
Ver solução completaQuestão 31
Sabe-se que um certo material radioativo se desintegra a uma taxa proporcional à quantidade presente. Observa-se que um bloco deste material, que originalmente tinha , depois de ficou apenas com r. Encontre uma expressão para a massa do bloco em função do tempo. Calcule a meia-vida do material.
Ver solução completaQuestão 32
Certa pessoa infectada por uma doença contagiosa introduziu-se numa população saudável
de pessoas. O mal se espalhou por contato, conseguindo-se deduzir a lei de propagação , onde tempo é medido em meses, é o número de pessoas infectadas no instante e é o número de pessoas não infectadas no instante t. Considerando que uma pessoa infectada permanecerá doente durante todo o tempo e que pessoas serão infectadas meses após o início do processo de contágio, pergunta-se: Quanto tempo será necessário para que a metade da população esteja infectada?
Ver solução completaQuestão 33
Uma cultura de bactérias cresce a uma taxa proporcional à quantidade presente. Ao fim
de , cresceu
- Determine a constante de proporcionalidade
Questão 34
Uma cultura de bactérias cresce a uma taxa proporcional à quantidade presente. Ao fim
de , cresceu
b) Quanto tempo levará a cultura para duplicar?
Ver solução completaQuestão 35
Determine uma família de curvas , que satisfazem a seguinte
propriedade: no intervalo , a ordenada é proporcional à área determinada pela
curva, os eixos coordenados e a reta vertical que contém a abcissa .
Ver solução completaQuestão 36
Certa substância radioativa decresce a uma taxa proporcional à quantidade presente. Se
observa que após , houve uma redução de da quantidade inicial. Determine
a meia-vida da substância (meia-vida de uma substância radioativa é o tempo que a
substância leva para que sua massa decaia à metade da quantidade original).
Ver solução completaQuestão 37
Indique a solução correta da equação diferencial:
( )
( )
( )
( )
( )
Ver solução completaQuestão 38
Resolva a equação diferencial para como função vetorial de
com a seguinte condição inicial:
Ver solução completaQuestão 39
Suponha que no instante , a metade de uma população de coelhos é infectada por um vírus que começa crescendo com uma taxa de coelhos por dia. Assumindo que a taxa com que o vírus se espalha é proporcional à quantidade de coelhos infectados vezes a quantidade de coelhos não infectados, determine o tempo que levará para que o vírus se espalhe por da população.
Ver solução completaQuestão 40
A taxa com que o virus da gripe "C" se espalha em uma comunidade é proporcional ao número de pessoas infectadas vezes o número de pessoas não infectadas. No início da prova de Cálculo 2 em uma sala com 60 alunos, tinham 3 alunos gripados e 2 horas depois 35 alunos estavam contaminados. Seja o número de pessoas gripadas após minutos e . O modelo matemático que melhor representa este problema é:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 41
3) Um objeto é retirado do freezer à temperatura de e colocado em um ambiente cuja temperatura é . Observou-se que depois de a temperatura do objeto era . Quanto tempo a mais será necessário para que a temperatura do objeto seja de ?
Ver solução completaQuestão 42
Devido a uma maldição rogada por uma tribo inimiga, os membros de uma certa aldeia
são gradualmente impelidos ao assassinato ou suicídio. A taxa de variação da população
é de , quando o número de pessoas é . Quando a maldição foi rogada a população era de pessoas. Quando morrerá toda a população da aldeia?
Ver solução completaQuestão 43
A população de uma comunidade cresce a uma taxa proporcional ao número de pessoas presentes em qualquer instante dada pela equação
Sabendo que a população inicial é e que a população duplicou em anos, qual é o valor de ?
Ver solução completaQuestão 44
Um tanque contém litros de água salgada com de sal dissolvido. Água salgada com de sal por lto de água entra no tanque a uma taxa de litros por minuto. A solução é mantida completamente misturada e sai do tanque a uma taxa de 10 litros por minuto.
- Escreva a equação diferencial que determina a taxa de variação da quantidade de sal em relação ao tempo.
- Determine a quantidade de sal no tanque minutos após o inicio.
- Determine a quantidade de sal no tanque minutos após o inicio.
- Calcule o limite da quantidade de sal no tanque quanto .
Questão 45
Uma cultura de bactérias começa com bactérias e cresce a uma taxa proporcional a seu tamanho. Após horas existem bactérias na amostra. Em horas serão:
- bactérias
- bactérias
- bactérias
- bactérias
- bactérias
Questão 46
Devido a uma maldição rogada por uma tribo inimiga, os membros de uma certa aldeia são gradualmente impelidos ao assassinato ou suicídio. A taxa de variação da população é de pessoas/mês, quando o número de pessoas é p. Quando a maldição foi rogada a população era de 1600 pessoas. Quando morrerá toda a população da aldeia?
Ver solução completaQuestão 47
Certa pessoa infectada por uma doença contagiosa introduziu-se numa população saudável de 999 pessoas. O mal se espalhou por contato, conseguindo-se deduzir a lei de propagação y’(t) = βyx onde t = tempo é medido em meses, y(t) é o número de pessoas infectadas no instante t e x(t) é o número de pessoas não infectadas no instante t. Considerando que uma pessoa infectada permanecerá doente durante todo o tempo e que 100 pessoas serão infectadas 12 meses após o início do processo de contágio, pergunta-se: Quanto tempo será necessário para que a metade da população esteja infectada?
Ver solução completaQuestão 48
Sabe-se que um certo material radioativo se desintegra a uma taxa proporcional à quantidade presente. Observa-se que um bloco deste material, que originalmente tinha 100gr, depois de 20 anos ficou apenas com 80gr. Encontre uma expressão para a massa do bloco em função do tempo. Calcule a meia-vida do material.
Ver solução completaQuestão 49
Suponha que a taxa de crescimento de uma certa população varia com o tempo, e que o número de indivíduos da mesma no instante satisfaz a equação diferencial:
i) Se encontre(ou estime) o instante no qual a população dobra.
Determine se o tempo no qual o número de indivíduos dobra dependa da população inicial.
ii) Suponha que a parcela na equação diferencial é substituída por , isto é, a variação na taxa de crescimento tem uma frequência substancialmente maior. Qual é o efeito dessa mudança no tempo de duplicação da população ?
Ver solução completa