Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.1 - Ex. 34

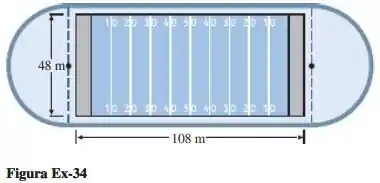
Um construtor de dependências esportivas quer colocar uma pista de corrida de um quarto de milha – 396 metros – em torno de um campo de futebol americano, conforme a figura a seguir. O campo de futebol tem 108 metros de comprimento (incluindo as zonas finais) por 48 metros de largura. A pista consiste em duas retas e dois semicírculos, sendo que as redes se estendem pelo menos ao longo do campo de futebol.

(a) Mostre que é possível construir a pista de um quarto de milha em torno do campo de futebol. [Sugestão: Encontre a menor pista que pode ser construída em torno do campo.]

(b) Seja L o comprimento de uma das partes retas (em metros) e x uma distância (em metros) entre a lateral do campo e a parte reta da pista. Faça um gráfico de L versus x.

(c) Use o gráfico para estimar o valor de x que produz a parte reta mais curta e então encontre exatamente esse valor.

(d) Use o gráfico para estimar o comprimento da maior parte reta possível e encontre exatamente esse comprimento.

Passo 1

(a) Vamos usar a sugestão e calcular qual a menor pista que pode ser construída em torno do campo.

Para saber qual a menor pista, vamos ter que calcular qual o menor comprimento em torno do campo. Vamos usar a própria imagem do problema:

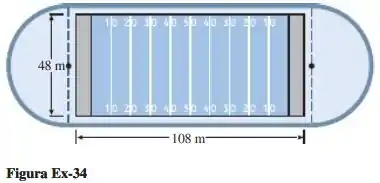
Olhando para ela, vemos que o comprimento em torno do campo é no mínimo igual ao comprimento das duas linhas retas e dos dois semicírculos. Cada linha reta tem e o comprimento de um semicírculo é (), sendo que os dois semicírculos são iguais:

Olhando para a figura, vemos que os diâmetros dos semicírculos são iguais a , logo, o raio . Com isso:

Como o comprimento mínimo da pista é e a pista que queremos construir tem , ou seja, ela é maior que a menor pista, é possível construí-la!!

Passo 2

(b) Temos essa situação:

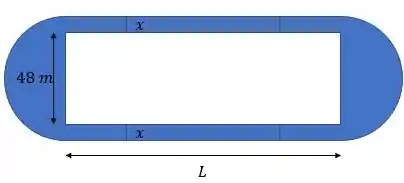
Bom, supondo que vamos construir a pista com de comprimento, temos que o comprimento da pista é:

Já que são as duas retas e os dois semicírculos. Só que, agora, e , pelo o que podemos ver na figura. Dessa forma:

Simplificando:

Como queremos em função de , vamos isolar :

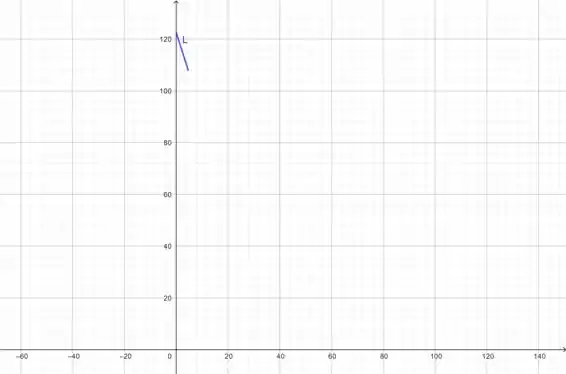
Plotando essa função, lembrando que nem não possuem valores negativos por serem medidas de comprimento e que tem que ser no mínimo (que é o comprimento do campo):

Passo 3

(c) Então, como vimos no passo anterior, deve ser no mínimo igual ao comprimento do campo . Senão, teremos uma pista menor que o campo e não dá para isso acontecer!