Uma empresa de construções acrescentou uma área retangular de mil metros quadrados à sua sede. Três lados da área estão cercados. O lado da sede que é adjacente à área mede 100 metros, e uma parte desse lado é utilizada como o quarto lado da área acrescentada. Sejam x e y as dimensões da área retangular, onde x é medido paralelamente à sede, e L o comprimento da cerca necessária para essas dimensões.
(a) Encontre uma fórmula para L em termos de x e y.
(b) Encontre uma fórmula que expresse L somente em termos de x.
(c) Qual é o domínio da função em (b)?
(d) Esboce o gráfico da função em (b) e estime as dimensões da área retangular que minimizem a quantidade de cerca necessária.
Passo 1
(a) Primeiro, vamos entender o que tá acontecendo:
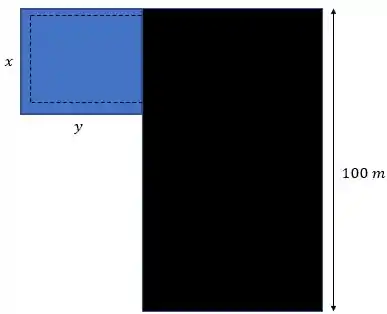
Em azul é a área retangular de e em preto é a sede com o lado de . (Como nada foi falado sobre o formato da sede, fiz ela retangular só pra ficar mais fácil de imaginar kk). Além disso, temos aonde teremos a cerca em pontilhado ali!
Logo pela figura, vemos que o pontilhado é formado por dois lados e um . Então, a cerca necessária tem um comprimento:
Passo 2
(b) Agora, vamos precisar saber uma relação entre e , pois já sabemos em função dos dois.
O enunciado nos deu que essa área retangular vale . Vamos usar isso, pois sabemos que a área de um retângulo é o produto dos seus lados:
Como :
Substituindo isso na equação para do passo anterior:
Ou ainda, fazendo o mmc:
Passo 3
(c) O domínio representa os valores de .
Olhando para a função que temos:
De cara, podemos dizer que , pois ficaria uma divisão por e não queremos isso. Além disso, como é uma medida de comprimento, não podemos ter um valor negativo para ele. Por último, como uma parte do lado de da sede é usado como o quarto lado do retângulo e esse quarto lado deve valer , ele deve ser no máximo também!
Juntando essas informações, vemos que:
Passo 4
(d) Esboçando :
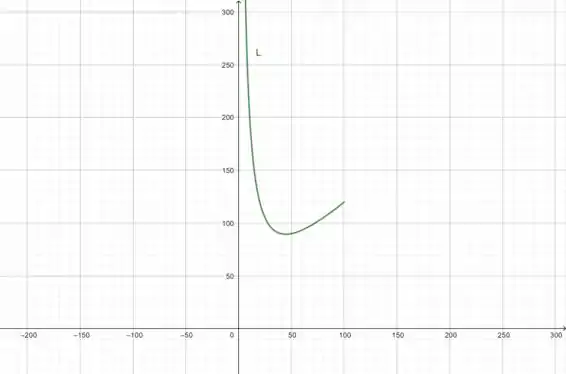
E vemos que o menor valor de ocorre entre e . Com isso, vamos colocar .
Dessa forma, usando a relação entre e do passo 2:
Resposta
(a)
(b)
(c)
(d) e