Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 3.2 - Ex. 33
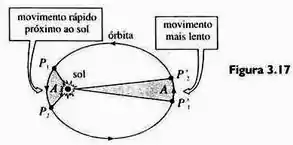
Em coordenadas polares, o momento angular de um corpo em movimento de massa é definido por . Suponha que as coordenadas do corpo sejam e nos intantes e , , respectivamente. Se é constante, mostre que a área varrida por é . Quando o sol é colocado na origem, isso prova a segunda lei de Kepler sobre movimento planetário.
Passo 1
Então pessoal, a equação que nos foi dada é a seguinte:
Para resolvermos essa equação é bem tranquilo, basta separarmos as variáveis e integrar depois, saca só:
Integrando:
Então bora que bora resolver issaí!
Passo 2
Multiplicando ambos os lados por , teremos:
O membro esquerdo da nossa equação é exatamente a área varrida, ou seja:
E está aí a demonstração!
Resposta
Demonstração.
Exercícios de Livros Relacionados
Nos problemas 41-54, resolva a equação diferencial dada sujeita à condição inicial indicada.41. d y d x + 5 y = 20 , no qual y 0 = 2 .
Nos problemas 1-40, encontre a solução geral para a equação diferencial dada. Especifique um intervalo no qual a solução geral é definida.37. x + 2 2 d y d x = 5 - 8 y - 4 x y
Nos problemas 1-40, encontre a solução geral para a equação diferencial dada. Especifique um intervalo no qual a solução geral é definida.34. y d x = y e y - 2 x d y
Nos problemas 41-54, resolva a equação diferencial dada sujeita à condição inicial indicada.52. s e nx . d y d x + cos x . y = 0 , no qual y - π 2 = 1 .
Nos problemas 41-54, resolva a equação diferencial dada sujeita à condição inicial indicada.50. x y ' + y = e x , no qual y 1 = 2 .