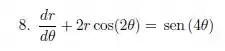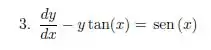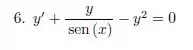Exercícios de EDO Linear de 1ª Ordem - Lista de Exercícios Resolvida
Questão 4
Encontre a solução geral para a equação diferencial dada. Especifique um intervalo no qual a solução geral é definida.
Ver solução completaQuestão 6
Classifique em Verdadeiro ou Falso a afirmação abaixo, justificando.
A equação diferencial
Tem exatamente duas soluções:
Ver solução completaQuestão 7
Resolva o problema de valor inicial abaixo, isto é, encontre a função ou as funções que satisfaz(em) a equação diferencial e as condições iniciais dadas.
Ver solução completaQuestão 8
Determine os valores de para os quais a equação diferencial dada tem uma solução da forma .
a)
Ver solução completaQuestão 9
Verifique que a função (ou funções) dada(s) é (são) solução (soluções) da equação diferencial.
c)
Ver solução completaQuestão 11
Considere o problema de valor inicial
- Resolva este problema para e
- O problema tem solução para ? Podemos usar o teorema da existência e unicidade para responder esta questão?
- Justifique que para o problema tem solução.
Questão 12
Verifique que a função (ou funções) dada(s) é (são) solução (soluções) da equação diferencial.
a)
Ver solução completaQuestão 14
01) Considere um circuito onde a força eletromotriz é uma constante , a capacitância é uma constante e a resistência aumenta linearmente, de modo que . Temos que as quedas de tensão no capacitor e na resistência são dadas, respectivamente, por e , onde é a carga no capacitor. A segunda Lei de Kirchoff diz que a soma das quedas de tensão em um circuito é igual à força eletromotriz.
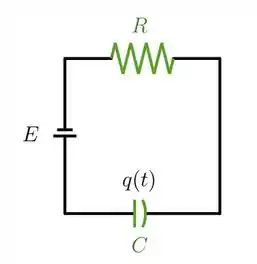
a) Mostre que a carga satisfaz uma equação da forma . Mostre também que a carga constante é uma solução, conhecida como carga estacionária.
Para os próximos itens considere .
b) Encontre uma primitiva de e determine e também .
c) Obtenha a solução geral da equação determinada no primeiro item.
d) Determine a solução com carga inicial . Mostre que, para qualquer carga inicial, após muito tempo decorrido a carga se aproxima da carga estacionária, isto é, mostre que .
Ver solução completaQuestão 17
Resolva as seguintes equações diferenciais, e problemas de valor inicial.
Ver solução completaQuestão 19
Determine os valores de para que a função seja uma solução para a equação diferencial .
O valor numérico de obtido é:
Ver solução completaQuestão 24
Resolva as seguintes equações diferenciais ou problemas de valor inicial, conforme seja o caso.
a)
Ver solução completaQuestão 25
- Determine a solução geral explícita da equação diferencial
- Utilize o resultado do item (a) para obter a solução do problema de valor inicial
Ver solução completaQuestão 27
Determine as soluções gerais, explicitas ou implícitas, das equações diferenciais
de 1ª ordem acima, com métodos apropriados para cada caso.
Ver solução completaQuestão 28
Determine explicitamente, ou indique implicitamente, a solução do problema de
valor inicial para cada equação diferencial de 1ª ordem acima, com a condição inicial :
Ver solução completaQuestão 29
Julgue em verdadeiro ou falso a seguinte afirmação:
“A equação diferencial é ordinária, não linear e de primeira ordem”
Verdadeiro ou falso?
Ver solução completaQuestão 32
Nos problemas de (a) até (l), encontre a solução geral da equação diferencial dada. Dê o maior intervalo I sobre o qual a solução geral está definida.
Ver solução completaQuestão 33
Nos problemas de (a) até (l), encontre a solução geral da equação diferencial dada. Dê o maior intervalo I sobre o qual a solução geral está definida.
Ver solução completaQuestão 34
Nos problemas de (a) até (l), encontre a solução geral da equação diferencial dada. Dê o maior intervalo I sobre o qual a solução geral está definida.
Ver solução completaQuestão 38
Nos problemas de (a) até (l), encontre a solução geral da equação diferencial dada. Dê o maior intervalo I sobre o qual a solução geral está definida.
Ver solução completaQuestão 39
Nos problemas de (a) até (l), encontre a solução geral da equação diferencial dada. Dê o maior intervalo I sobre o qual a solução geral está definida.
Ver solução completaQuestão 40
Questão 1: Resolva as seguintes equações diferenciais e problemas de valor inicial, conforme seja o caso:
Ver solução completaQuestão 42
Marque a alternativa que indica a solução do problema de Valor inicial
( )
( )
( )
( )
( )
Ver solução completaQuestão 43
Dada uma ED ; , indique qual é o único fator de integração correto:
( )
( )
( )
( )
( )
Ver solução completaQuestão 46
Resolva os problemas de valor inicial abaixo, indique o intervalo de validade da solução encontrada e esboce seu gráfico:
Ver solução completaQuestão 49
Nos problemas de (a) até (l), encontre a solução geral da equação diferencial dada. Dê o maior intervalo I sobre o qual a solução geral está definida.
Ver solução completaQuestão 50
Nos problemas de (a) até (c), resolva o problema de valor inicial. Dê o maior intervalo sobre o qual cada solução está definida
Ver solução completaQuestão 51
Nos problemas de (a) até (l), encontre a solução geral da equação diferencial dada. Dê o maior intervalo I sobre o qual a solução geral está definida.
Ver solução completaQuestão 52
Nos problemas de (a) até (l), encontre a solução geral da equação diferencial dada. Dê o maior intervalo I sobre o qual a solução geral está definida.
Ver solução completaQuestão 53
Nos problemas de (a) até (c), resolva o problema de valor inicial. Dê o maior intervalo sobre o qual cada solução está definida
Ver solução completaQuestão 55
Nos problemas de (a) até (c), resolva o problema de valor inicial. Dê o maior intervalo sobre o qual cada solução está definida
Ver solução completaQuestão 56
Encontre o valor de para o qual a solução do problema de valor inicial:
permanece finita quando
Ver solução completaQuestão 69
Resolva o problema de valor inicial
, .
E determine onde a solução atinge seu valor máximo.
Ver solução completaQuestão 70
Para cada equação abaixo encontre a solução do problema de valor inicial em forma explícita.
f), .
Ver solução completaQuestão 71
Resolva o problema de valor inicial
, .
E determine onde a solução atinge seu valor máximo.
Ver solução completaQuestão 72
Julgue em verdadeiro ou falso a seguinte afirmação:
“A equação diferencial é ordinária, linear e de segunda ordem”
Verdadeiro ou falso?
Ver solução completaQuestão 73
Dada a equação diferencial a seguir, complete a frase de forma a deixa-la verdadeira.
“A equação diferencial é...”
Ver solução completaQuestão 74
Dada a equação diferencial a seguir, complete a frase de forma a deixa-la verdadeira.
“A equação diferencial é...”
Ver solução completaQuestão 75
Julgue em verdadeiro ou falso a seguinte afirmação:
“A equação diferencial é ordinária, não linear e de primeira ordem”
Verdadeiro ou falso?
Ver solução completaQuestão 76
Julgue em verdadeiro ou falso a seguinte afirmação:
“A equação diferencial é ordinária, não linear e de quarta ordem”
Verdadeiro ou falso?
Ver solução completaQuestão 78
Nos problemas de (a) até (l), encontre a solução geral da equação diferencial dada. Dê o maior intervalo I sobre o qual a solução geral está definida.
Ver solução completaQuestão 85
Dada a equação diferencial a seguir, complete a frase de forma a deixa-la verdadeira.
“A equação diferencial é...”
Ver solução completaQuestão 86
Considere as afirmações:
Todas as soluções da equação são decrescentes.
A equação é separável.
A função é um fator integrante para a equação .
Escolha uma:
Somente e são falsas.
As afirmações e são verdadeiras.
Todas as afirmações são falsas.
As afirmações e são verdadeiras.
Somente e são falsas.
Ver solução completaQuestão 87
Julgue em verdadeiro ou falso a seguinte afirmação:
“A equação diferencial é ordinária, não linear e de quarta ordem”
Verdadeiro ou falso?
Ver solução completaQuestão 89
Calcule e de modo que satisfaça as condições dadas:
Explique se tais condições caracterizam um Problema de Valor Inicial ou de Valor de Contorno. Marque a única resposta correta.
Ver solução completa
Questão 90
Resolva o problema de valor inicial abaixo, isto é, encontre a função ou as funções que satisfaz(em) a equação diferencial e as condições iniciais dadas.
Ver solução completaQuestão 92
Considere um circuito RLC onde a força eletromotriz é , a resistência é , a indutância é e a capacitância é . Temos que a queda de tensão no indutor, no capacitor e na resistência é dada, respectivamente, por , onde q(t) é a carga no capacitor. A segunda Lei de Kirchoff afirma que a soma das quedas de tensão num circuito é igual à força eletromotriz.
a) Mostre que a carga no capacitor satisfaz uma EDO linear de segunda ordem.
b) Verifique que e são soluções fundamentais da equação homogênea.
c) Obtenha a solução geral da equação não homogênea. A carga no capacitor tende a zero quando t cresce?
d) Determine a carga q(t) do capacitor se a carga inicial é e a corrente inicial é .
Ver solução completaQuestão 93
04) Num foguete, se o empuxo é uma constante , a taxa de variação de sua massa é constante, de modo que . Se o foguete não atinge uma altura muito elevada, podemos supor que a gravidade é uma constante e que a força de arraste do ar é dada por , proporcional à velocidade do foguete. Segue que a força que atua no foguete é dada por:
Neste caso, a segunda lei de Newton é dada por:
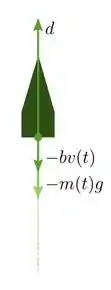
a) Mostre que satisfaz uma equação da forma .
Para os próximos itens considere .
b) Encontre uma primitiva de e determine e também .
c) Obtenha a solução geral da equação determinada no primeiro item.
d) Determine a solução com velocidade inicial . Para que valores de a velocidade está definida?
Ver solução completaQuestão 94
05) Vamos investigar a dinâmica, num dado país, da relação entre a renda produzida no tempo e o capital acumulado até o tempo através do famoso modelo Solow-Swan. Temos que a renda é dada por uma função Cobb-Douglas do capital e do trabalho, de modo que:
E que o capital se acumula por uma taxa de poupança constante positiva e se deprecia a uma taxa constante positiva , de modo que:
Denotando a renda e o capital per capita, respectivamente, por e por , a taxa de crescimento do trabalho por , a razão riqueza pela renda no tempo por e o seu limite quando tende por infinito por , responda os seguintes itens.
a) Mostre que .
b) Use o item anterior para mostrar que .
c) Mostre que e conclua que
d) Use os itens anteriores para mostrar que
e) Supondo que constante e que , mostre que:
f) Conclua que .
Ver solução completaQuestão 95
01) A temperatura de equilíbrio em um ponto de uma chapa circular feita com um material uniforme pode ser escrita em função das coordenadas polares , de , onde é a distância entre o ponto e a origem e é o ângulo formado entre o eixo e o segmento . Temos que varia em e que varia em , onde é o raio da chapa. Note que o conjunto dos pontos tais que é constante formam uma circunferência.
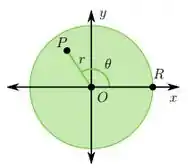
Escrevendo a temperatura em como produto de duas funções , é possível mostrar que as funções e satisfazem as seguintes equações diferenciais:
Onde é uma constante positiva. O objetivo dessa questão é resolver essas duas equações diferenciais e estudar suas soluções.
a) Mostre que satisfaz a equação . Determine os valores de tais que e são soluções fundamentais dessa equação.
b) Use o fato de que e representam o mesmo ponto na chapa, para concluir que . Use esse fato para concluir que , para algum inteiro .
c) Mostre que satisfaz a equação , , conhecida como equação de Euler. Determine os valores de tais que é solução da equação de Euler.
d) Use o item anterior para obter a solução geral da equação de Euler. Verifique que qualquer solução que não é proporcional à solução possui assíntota vertical em .
Ver solução completaQuestão 96
Determine os pontos , para os quais podemos garantir que o problema de valor inicial , tem solução única.
(e) Se
Ver solução completaQuestão 97
Resolva a equação diferencial dada usando uma substituição apropriada.
(i)
Ver solução completaQuestão 98
Nos problemas de (a) até (l), encontre a solução geral da equação diferencial dada. Dê o maior intervalo I sobre o qual a solução geral está definida.
Ver solução completaQuestão 99
Considere o problema de valor inicial , . O valor de é igual a
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 100
Determine se aa equação diferencial ordinária (EDO) de primeira ordem é linear
Ver solução completaQuestão 101
Determine se a equação diferencial ordinária (EDO) de primeira ordem é linear
Ver solução completaQuestão 102
Suponha que é uma solução da equação . Determine a solução geral da equação.
Ver solução completaQuestão 103
Questão 2: (Justifique todas as suas respostas)
Considere o PVI
Encontre o valor de para o qual a solução deste PVI permanece finita conforme .
Ver solução completaQuestão 106
2) Uma colônia de bactérias obedece a “lei natural da evolução” (Lei de Malthus), isto é, a taxa de crescimento populacional é proporcional à população. Observou-se que há atrás havia bactérias, e que agora há cerca de .
a) Apresente a equação que fornece a quantidade de bactérias na hora .
Ver solução completaQuestão 109
2) Uma colônia de bactérias obedece a “lei natural da evolução” (Lei de Malthus), isto é, a taxa de crescimento populacional é proporcional à população. Observou-se que há atrás havia bactérias, e que agora há cerca de .
b) Qual a população de bactérias daqui a horas?
Ver solução completaQuestão 110
2) Uma colônia de bactérias obedece a “lei natural da evolução” (Lei de Malthus), isto é, a taxa de crescimento populacional é proporcional à população. Observou-se que há atrás havia bactérias, e que agora há cerca de .
c) Daqui a quanto tempo a população atingirá bactérias?
Ver solução completaQuestão 112
A velocidade de um ponto material que se move ao longo de uma linha reta é diretamente proporcional ao tempo do movimento e inversamente proporcional à distância até a origem. Encontre a trajetória de um ponto se, no instante inicial do tempo, a distância até a origem for , ou seja .
Ver solução completaQuestão 113
Determine se a equação diferencial ordinária (EDO) de primeira ordem é linear
Ver solução completaQuestão 114
Suponha que é contínua em algum intervalo I e é um número em I. O que pode ser dito a respeito da solução do PVI ?
Ver solução completaQuestão 115
- Construa uma equação diferencial linear de primeira ordem da forma para qual e . Dê um intervalo sobre o qual é a solução geral da EDO
- Defina uma condição inicial para a EDO encontrada na parte (a) tal que a solução do PVI seja . Redefina a condição inicial se a solução é . Dê um intervalo I de definição de cada uma dessas soluções. Existe um problema de valor inicial cuja solução está definida sobre ?
- Cada PVI encontrado na parte (b) é único? Isto é, pode existir mais do que um PVI para o qual, digamos, , em algum intervalo I, é solução?
Ver solução completaQuestão 116
A solução da equação diferencial , com , e que passa pelo ponto verifica:
(a)
(b)
(c) Nenhuma das opções
(d)
(e) é decrescente em
Ver solução completaQuestão 117
Considere o problema de valor inicial
Sabendo que é um fator integrante desta equação diferencial e que a solução do problema acima é ache .
Ver solução completaQuestão 118
Questão 1 (Justifique todas as suas respostas):
Encontre a solução do problema de valor inicial:
e estude o seu comportamento .
Ver solução completaQuestão 119
Resolva a seguinte equação diferencial ou problema de valor inicial conforme seja o caso:
Questão 124
Resolva o problema de valor inicial
, .
E determine onde a solução atinge seu valor mínimo.
Ver solução completaQuestão 129
1) A corrente em um circuito elétrico com indutância e resistência é dada pela equação
Onde é a tensão aplicada. Suponha que e são constantes (arbitrárias; não especifique), e que seja dada por , sendo e também constantes (arbitrárias; não especifique). Encontre .
Ver solução completaQuestão 130
- Determine a solução geral da EDO
E determine o comportamento da solução quando em função da constante
Ver solução completaQuestão 131
Marque a alternativa que indica a solução do problema de valor inicial:
( )
( )
( )
( )
( )
Ver solução completaQuestão 132
Determine a solução do problema de valor inicial dado em forma explícita
Ver solução completaQuestão 134
Encontre o fator integrante correto para a seguinte equação diferencial:
Questão 136
Nos problemas abaixo indique o intervalo que contém a condição inicial no qual as hipóteses do teorema de existência e unicidade de soluções de EDOs lineares de ordem são verdadeiras:
Ver solução completaQuestão 137
Nos problemas abaixo indique o intervalo que contém a condição inicial no qual as hipóteses do teorema de existência e unicidade de soluções de EDOs lineares de ordem são verdadeiras:
Ver solução completaQuestão 138
Nos problemas abaixo indique o intervalo que contém a condição inicial no qual as hipóteses do teorema de existência e unicidade de soluções de EDOs lineares de ordem são verdadeiras:
Ver solução completaQuestão 139
Determine as regiões do plano nas quais as hipóteses do teorema de existência e unicidade de soluções de EDOs de primeira ordem são satisfeitas:
Ver solução completaQuestão 140
Resolva os problemas de valor inicial abaixo, indique o intervalo de validade da solução encontrada e esboce seu gráfico:
Ver solução completaQuestão 141
Determine as regiões do plano nas quais as hipóteses do teorema de existência e unicidade de soluções de EDOs de primeira ordem são satisfeitas:
Ver solução completaQuestão 142
Determine as regiões do plano nas quais as hipóteses do teorema de existência e unicidade de soluções de EDOs de primeira ordem são satisfeitas:
Ver solução completaQuestão 144
Resolva os problemas de valor inicial abaixo, indique o intervalo de validade da solução encontrada e esboce seu gráfico:
Ver solução completaQuestão 148
Resolva os problemas de valor inicial abaixo, indique o intervalo de validade da solução encontrada e esboce seu gráfico:
Ver solução completaQuestão 149
Resolva os problemas de valor inicial abaixo, indique o intervalo de validade da solução encontrada e esboce seu gráfico:
Ver solução completaQuestão 150
Considere o problema de valor inicial:
Resolva o problema de valor inicial e esboce as soluções quando:
Questão 151
Considere uma equação diferencial da forma
Faça a mudança de variáveis afim de obter a equação separável:
Ver solução completaQuestão 152
Considere o problema de valor inicial:
Qual o intervalo de definição da solução se Podemos esperar algum comportamento assintótico da solução neste caso?
Ver solução completaQuestão 153
Considere uma equação diferencial da forma
Utilize esta mudança de variáveis para resolver a equação diferencial
Ver solução completaQuestão 154
Determine a solução do problema de valor inicial dado em forma explícita
Ver solução completaQuestão 156
Determine o maior intervalo em que os problemas de valor inicial abaixo têm solução
Ver solução completaQuestão 157
03) Considere um circuito RC onde a força eletromotriz é uma constante , a capacitância é dada por e a resistência é dada por . Temos que as quedas de tensão no capacitor e na resistência são dadas, respectivamente, por e , onde é a carga no capacitor. A segunda lei de Kirchoff diz que a soma das quedas de tensão num circuito é igual à força eletromotriz.
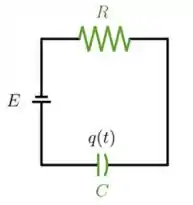
a) Mostre que a carga satisfaz uma equação da forma .
b) Encontre uma primitiva de e determine e também .
c) Obtenha a solução geral da equação determinada no primeiro item.
d) Determine a solução com carga inicial . Mostre que mostrando que esse limite não depende da carga inicial .
Ver solução completaQuestão 159
Resolva cada um dos seguintes problemas de valores iniciais. Para isso encontre uma primitiva que seja solução da equação diferencial dada e imponha as condições dadas de modo de determinar a constante de integração do caso geral.
Ver solução completaQuestão 160
Resolva cada um dos seguintes problemas de valores iniciais. Para isso encontre uma primitiva que seja solução da equação diferencial dada e imponha as condições dadas de modo de determinar a constante de integração do caso geral.
Ver solução completaQuestão 162
Resolva cada um dos seguintes problemas de valores iniciais. Para isso encontre uma primitiva que seja solução da equação diferencial dada e imponha as condições dadas de modo de determinar a constante de integração do caso geral.
Ver solução completaQuestão 169
Determine a solução do problema de valor inicial dado em forma explícita
Ver solução completaQuestão 170
Determine a solução do problema de valor inicial dado em forma explícita
Ver solução completaQuestão 172
Determine a solução do problema de valor inicial dado em forma explícita
Ver solução completaQuestão 173
Determine a solução do problema de valor inicial dado em forma explícita
Ver solução completaQuestão 181
Determine a solução do problema de valor inicial dado em forma explícita
Ver solução completaQuestão 182
Determine a solução do problema de valor inicial dado em forma explícita
Ver solução completaQuestão 183
Determine a solução do problema de valor inicial dado em forma explícita
Ver solução completaQuestão 184
Determine a solução do problema de valor inicial dado em forma explícita
Ver solução completaQuestão 186
Resolva a equação diferencial dada usando uma substituição apropriada.
(b)
Ver solução completaQuestão 187
Resolva a equação diferencial dada usando uma substituição apropriada.
(a)
Ver solução completaQuestão 188
Resolva a equação diferencial dada usando uma substituição apropriada.
(c)
Ver solução completaQuestão 189
Resolva a equação diferencial dada usando uma substituição apropriada.
(e)
Ver solução completaQuestão 190
Resolva a equação diferencial dada usando uma substituição apropriada.
(f)
Ver solução completaQuestão 191
Resolva a equação diferencial dada usando uma substituição apropriada.
(d)
Ver solução completaQuestão 192
Resolva a equação diferencial dada usando uma substituição apropriada.
(g)
Ver solução completaQuestão 193
Determine os pontos , para os quais podemos garantir que o problema de valor inicial , tem solução única.
(b) Se
Ver solução completaQuestão 194
Resolva a equação diferencial dada usando uma substituição apropriada.
(h)
Ver solução completaQuestão 195
Resolva a equação diferencial dada usando uma substituição apropriada.
(j)
Ver solução completaQuestão 196
Determine os pontos , para os quais podemos garantir que o problema de valor inicial , tem solução única.
(a)Se
Ver solução completaQuestão 197
Determine os pontos , para os quais podemos garantir que o problema de valor inicial , tem solução única.
(c) Se
Ver solução completaQuestão 198
Determine os pontos , para os quais podemos garantir que o problema de valor inicial , tem solução única.
(d) Se
Ver solução completaQuestão 199
Determine os pontos , para os quais podemos garantir que o problema de valor inicial , tem solução única.
(f) Se
Ver solução completaQuestão 200
UM circuito elétrico composto por um resistor (de resistência ), um indutor (de indutância ) e uma bateria (com diferença de potencial entre os seus terminais) está ilustrado abaixo.
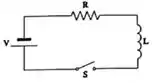
A chave est inicialmente aberta e, consequentemente, não há corrente elétrica passando pelo circuito. No instante , essa chave é ligada e a corrente que atravessa o circuito é solução da seguinte equação diferencial:
Onde são constantes positivas. A expressão que define a corrente , para um instante qualquer, é:
Questão 201
Determine o maior intervalo em que os problemas de valor inicial abaixo têm solução
Ver solução completaQuestão 202
Determine o maior intervalo em que os problemas de valor inicial abaixo têm solução
Ver solução completaQuestão 203
Determine o maior intervalo em que os problemas de valor inicial abaixo têm solução
Ver solução completaQuestão 204
Determine se a equação diferencial ordinária (EDO) de primeira ordem é linear
Ver solução completaQuestão 205
Seja a equação diferencial . Qual dentre as opções abaixo não é uma solução da equação diferencial proposta, sabendo que y=f(x) ?
( )
( )
( )
( )
( )
Ver solução completaQuestão 207
Questão 1: (Justifique todas as suas respostas)
Determine se cada uma das afirmações abaixo é Verdadeira ou Falsa:
- Considere a equação
Sempre é possível obter um fator integrante para esta equação.
Ver solução completa