Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.4 - Ex. 15
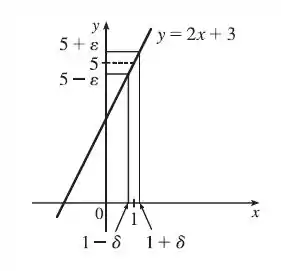
Demonstre cada afirmação usando a definição , de limite e ilustre com um diagrama como o da Figura 9.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá o seguinte limite:
Queremos demonstrar essa igualdade utilizando os conceitos de e .
A questão também nos pede para ilustrar o limite dado com um diagrama como o da seguinte figura:
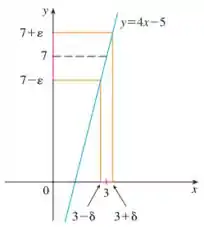
Bom... vamos lembrar alguns conceitos antes:
“Seja uma função definida em algum intervalo o aberto que contenha o número a, exceto possivelmente no próprio . Então dizemos que o limite de quando tende a é , e escrevemos:
Se para todo número houver um número tal que
Se então .”
Agora bora lá!! 😉
Passo 2
Dado que , nós precisamos achar , tal que se:
Então, temos que:
Vamos agora simplificar isso:
Passo 3
Resumindo o passo anterior, temos que se:
Então:
Passo 4
Isso nos dá que se nós escolhemos , e substituirmos seu valor, temos que
Podemos dizer que , portanto:
Portanto, temos o limite
pelo limite da definição.
Passo 5
Aqui temos o diagrama:
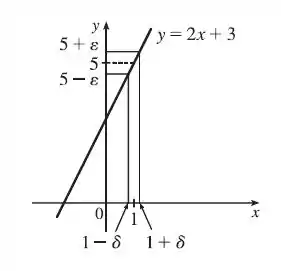
Resposta
