Demonstre cada afirmação usando a definição , de limite e ilustre com um diagrama como o da Figura 9.
Passo 1
Bom galerinha!
Já que a gente precisa fazer uma demonstração usando a definição de limite, vamos relembrar dessa definição.
Quando a gente tá falando de limite, não estamos no ponto , nós estamos beeem pertinho dele. Mas sobre isso a gente já tá bem tranquilo ne?
Quão próximo de deverá estar para que difira de por menos que uma tolerância bem pequeno ?

Em palavras mais fáceis e menos assustadoras, a gente tá dizendo que pra existir esse limite:
A gente precisa provar o seguinte:
Que dado um pequeno intervalo ao redor de , há de conseguir achar um valorzinho pra , que qualquer dentro desse outro intervalinho retorne na função um valor dentro do primeiro intervalo .
Na prática, você precisa dessas duas inequações que aparecem ali dentro da caixinha rosa:
se então
Agora aplicando isso na nossa expressão:
se então
Agora nós precisamos achar que atenda essas condições!
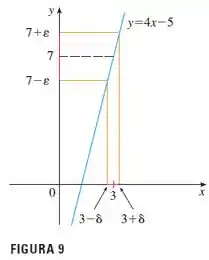
Mas antes de começar, vamos ver o diagrama da figura 9 que o enunciado menciona. Nele da pra ver bem esses intervalos nos 2 eixos e essa história de que um dentro de um intervalo tem que retornar um dentro do outro intervalo. Mas ignora esses números da figura, isso é só o exemplo que o livro usou.
Passo 2
Vamos agora simplificar isso:
Abrindo o módulo:
Agora vamos transformar o 3 em -3:
Opa isso aqui tá bem parecido com aquilo que a gente queria encontrar hein, olha só!
A gente tava procurando um valor que atendesse à seguinte inequação:
Pronto, achamos
Passo 3
Agora vamos fazer o caminho contrário.
Se nós escolhemos , e substituirmos seu valor, temos que:
Reorganizando
Agora vamos manipular mais um pouquinho pra aparecer o que a gente quer:
Pronto, nosso valor qualquer dentro do intervalinho retornou na função um valor dentro do primeiro intervalo .
Uhuuulll!
Provamos que o limite existe!
Passo 4
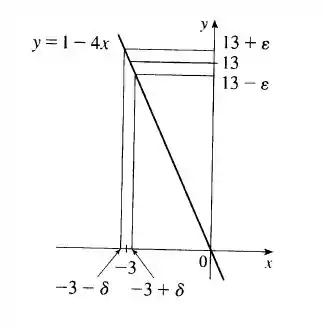
Aqui temos o diagrama, com os intervalos definidor nos dois eixos:
Resposta
Demonstração