Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.1 - Ex. 4
(a) Estime a área sob o gráfico de de até usando quatro retângulos aproximantes e extremidades direitas. Esboce o gráfico e os retângulos. Sua estimativa é uma subestimativa ou uma superestimativa?
(b) Repita a parte (a) usando extremidades esquerdas.
Passo 1
Eaee, belezinha?? Bom... queremos estimar a área sob o gráfico da seguinte função:
No intervalo de até usando quatro retângulos aproximantes e extremidades direitas.
Assim, devemos esboçar o gráfico e os retângulos e concluir se nossa estimativa é uma subestimativa ou uma superestimativa.
Depois, temos que fazer a mesma coisa, mas utilizando as extremidades esquerdas.
Para isso, devemos primeiro plotar a nossa função:
Agora vamos responder o que o enunciado está nos pedindo!!
Passo 2
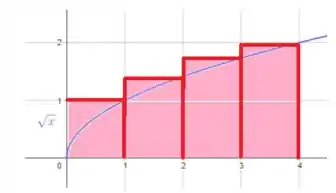
Selecionando os quatro retângulos aproximantes e extremidades direitas, isso quer dizer que vamos desenhar os retângulos de maneira que seus vértices superiores diretos interceptem o gráfico da função.
Com isso, temos:
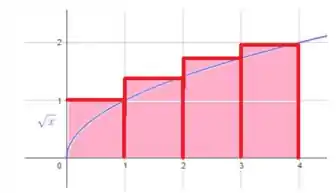
Estimando a área:
Como está crescendo em , é obtida uma superestimação em .
Passo 3
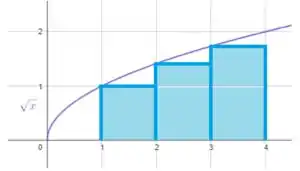
Agora vamos fazer o mesmo, mas como o vértice superior esquerdo dos retângulos interceptando o gráfico da função.
Assim, o esboço do gráfico é o seguinte:
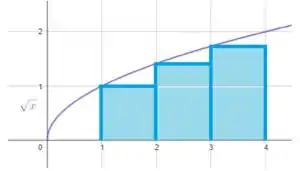
Estimando a área:
é uma subestimação.
Entendeu direitinho?? Responde aee 😉
Resposta
a)
Superestimada
b)
Subestimada
