Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.3 - Ex. 35
Demonstre a fórmula para a área de um setor circular com raio e ângulo central .
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente demonstrar que a área de um setor circular de raio e ângulo central , é dada por .
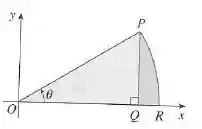
Para isso, vamos usar a figura que o enunciado nos deu:
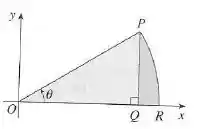
Vamos dividir a figura em duas áreas, a primeira é a área do triângulo com um sombreado mais claro. A segunda área será o setor circular, onde a função que define a curva é a equação da circunferência:
Com isso, vamos isolar , calcular a segunda área , através da integral e somar com a primeira área .
Vamos lá!
Passo 2
Podemos calcular a primeira área, usando a fórmula de área do triângulo (). Assim, temos:
Passo 3
Para a segunda área, primeiramente precisamos encontrar uma função que define a curva e depois integramos pra calcular a área. Como a função que define a curva é um circulo, temos:
Então, podemos isolar da seguinte forma:
Agora vamos integrar essa função para encontrar nossa área:
Passo 4
Vamos resolver esta integral fazendo uma substituição trigonométrica. Fazendo:
Diferenciando, temos que :
Precisamos calcular os novos limites de integração:
Substituindo na integral, temos:
Usando a identidade trigonométrica :
Cortando a raiz com o expoente ao quadrado e multiplicando os termos, temos:
Como a integral é em relação a , podemos colocar o termo que tem do lado de fora da integral:
Assim, integrando, teremos:
E aplicando os limites de integração:
Passo 5
Agora, para encontrar a área total, basta somarmos as áreas. Então:
Simplificando:
Como queríamos demonstrar.
Valeu, galera! Até a próxima! 😉