Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.6 - Ex. 27
Descreva a mudança no gráfico de à medida que varia. Faça o gráfico de vários membros da família para ilustrar as tendências que você descobriu. Em particular, você deve imaginar como os pontos de máximo e mínimo e os pontos de inflexão movem-se quando varia. Você deve também identificar qualquer valor intermediário de no qual o aspecto básico da curva mude.
Passo 1
Oieee galerinhaa, tudo bemm?
Bora resolver essa questãozinha comigo?
Para iniciar a questão vamos relembrar um pouco da teoria:
Interseções com os Eixos:
- Eixo : Onde
- Eixo : Onde ou seja,
Derivadas e Comportamento da Função:
- Primeira Derivada Para determinar onde a função é crescente ou decrescente.
- Segunda Derivada Para determinar a concavidade e pontos de inflexão.
Os intervalos nos quais uma função é crescente (ou decrescente) correspondem aos intervalos nos quais sua derivada é positiva (ou negativa). Então, se quisermos encontrar os intervalos em que uma função é crescente ou decrescente, nós calculamos sua derivada e descobrimos onde ela é positiva ou negativa (o que é mais fácil!).
Concavidade e Pontos de Inflexão:
- Concavidade para cima:
- Concavidade para baixo:
- Pontos de Inflexão: Onde e muda de sinal.
Bora lá!! 😉
Passo 2
Podemos escrever a função como
Note que é uma função par.
Para o único ponto de interseção com o eixo é o ponto (0,0)
Calculando a primeira derivada
Calculando a segunda derivada
Se , é o único ponto crítico e não existe ponto de inflexão
Passo 3
Fazendo e para encontrar os pontos críticos.
Para , é o único ponto crítico e não existe ponto de inflexão
Para o gráfico é uma simples curva
Para o gráfico corta o eixo em .
Também existe um ponto de máximo em e um mínimo em
Não existe mudança na aparência do gráfico para , simplesmente se torna mais íngreme à medida que aumenta.
Quando as coordenadas no eixo do ponto de mínimo se tornam maiores no valor absoluto e estes pontos de mínimo se movem para baixo.
Existe um ponto de inflexão em que também se move para longe da origem quando
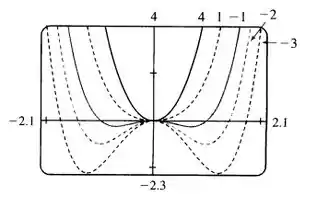
Resposta
Vide o passo a passo.