Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 5.1 - Ex. 3
(a) Estime a área sob o gráfico de de até usando quatro retângulos aproximantes e extremidades direitas. Esboce o gráfico e os retângulos. Sua estimativa é uma subestimativa ou uma superestimativa?
(b) Repita a parte (a) usando extremidades esquerdas.
Passo 1
Nessa questão temos que encontrar a área abaixo da função
Indo de até .
E para isso vamos utilizar retângulo e calcular a área desses retângulos.
Vamos usar que a área de um retângulo é dada como:
Onde a base vai ser a variação em de cada retângulo e a altura será o valor da função calculada no valor de da extremidade direita do retângulo (para a letra a)) e da extremidade esquerda do retângulo (para a letra b)).
Passo 2
O esboço do gráfico é o seguinte:
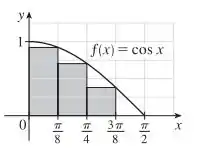
Estimando a área:
Como está decrescendo em , é obtida uma subestimação usando as aproximações extremas à direita .
Você pode ver isso ao verificar que as áreas dos retângulos quando somadas é menor que a área total abaixo da curva.
Passo 3
Para a letra b), teremos o esboço do gráfico a seguir:
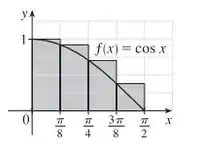
Estimando a área:
é uma superestimação.
Resposta
Para a letra a)
Subestimativa
Para a letra b)
Superestimativa