Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.3 - Ex. 38c

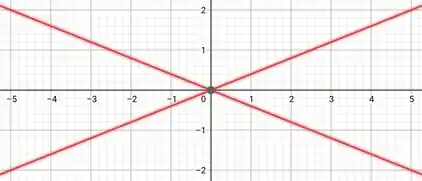
Desenhe um esboço do gráfico da equação:

4 * x^2 - 25 * y^2 = 0

Passo 1

Utilizando a fatoração diferença de quadrados ( a^2 - b^2 = (a + b) * (a - b) ), percebemos que essa equação representa duas retas simultaneamente. Para fazer esse gráfico, vamos encontrar dois pontos de uma das retas e ligá-los e repetir o processo com a outra reta.

Passo 2

( 2 * x )^2 - (5 * y)^2 = 0

(2 * x + 5 * y) * (2 * x - 5 * y) = 0

2 * x + 5 * y = 0 vv 2 * x - 5 * y = 0

Passo 2

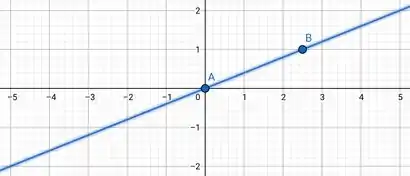
Para a primeira reta, quando x = 0 => 2 * 0 + 5 * y = 0 => y = 0 e quando y = 1 => 2 * x + 5 * 1 = 0 => x = - (5)/(2) .

Passo 3

Assim, marcamos os pontos (0 , 0) e (- (5)/(2) , 1) no gráfico e ligamos.

Passo 5

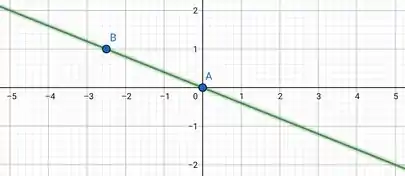
Para a segunda reta, quando x = 0 => 2 * 0 - 5 * y = 0 => y = 0 e quando y = 1 => 2 * x - 5 * 1 = 0 => x = (5)/(2) .

Passo 6

Assim, marcamos os pontos (0 , 0) e ((5)/(2) , 1) no gráfico e ligamos.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desenhe um esboço do gráfico da equação: y = sqrt(- 2 * x)
Desenhe um esboço do gráfico da equação: y = - sqrt(- 2 * x)
Desenhe um esboço do gráfico da equação: y^2 = - 2 * x
Desenhe um esboço do gráfico da equação: x^2 + y^2 = 4
Desenhe um esboço do gráfico da equação: y = sqrt(4 - x^2)