Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 68b
Ache todos os valores de t no intervalo de para os quais a equação dada é satisfeita:
b)
Passo 1
Queremos obter os ângulos (valores de t) no intervalo de que tenham seu cosseno igual a -1.
Para começar vamos desenhar nosso circulo trigonométrico, cujo raio é igual a 1.
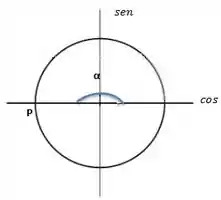
Como o raio do círculo é igual a 1, há somente um ponto P cujo ângulo α apresenta cosseno igual a -1. Então:
Passo 2
Sabendo os valores que podem ser assumidos pelo t nos resta descobrir qual é o valor do ângulo . Para isto, podemos usar a calculadora científica para calcular o arco cosseno de -1 ou simplesmente observamos no círculo. Obtemos então:
Sendo assim:
Em radianos:
Agora podemos calcular nosso t. Substituindo o valor de
Resposta
Exercícios de Livros Relacionados
Determine o valor exato da função s e c - 1 6 π .
Determine o valor exato da função c o s e c - 1 3 π .
Determine o valor exato da função c o t g 1 4 π .
Determine o valor exato da função s e c - π .
Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ( t ) , s e c ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da