Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 16
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Essas funções racionais são traiçoeiras, as vezes dá pra simplificar elas e ficar com uma função mais fácil de trabalhar. Podemos reescrever a como:
E agora temos uma diferença de quadrados no numerador! Podemos reescrever isso assim:
Simplificando, ficamos com a bem mais amigável:
Agora fica fácil determinar tudo que a função quer!
Passo 2
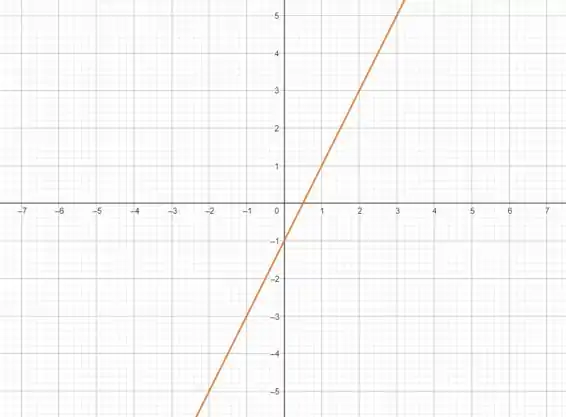
A nossa equação é um polinômio do 1º grau, o gráfico será uma reta! E ainda mais, já sabemos que o domínio é todo o conjunto e a imagem também.
Passo 3
Para plotar o gráfico de uma reta precisamos de apenas 2 pontos que pertençam à reta e depois desenhamos a reta que passa por esses dois pontos. Escolhendo dois pontos arbitrários, vamos fazer e :
E
Temos os dois pontos e . No plano cartesiano:
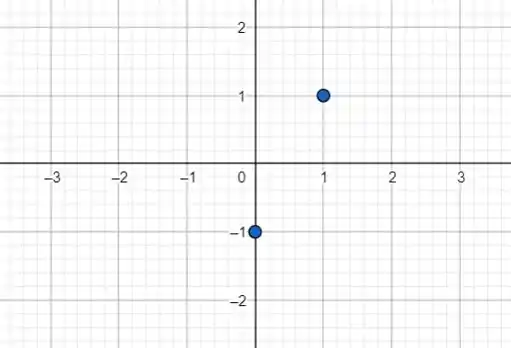
Agora é só traçar a reta que liga os dois pontos e temos o gráfico da nossa função:
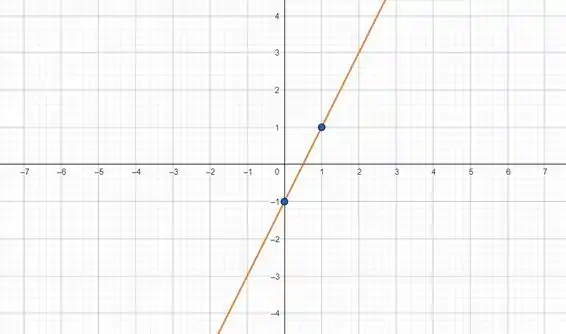
A reta laranja é o gráfico da nossa função!
Resposta
Domínio:
Imagem:
