Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.1 - Ex. 14

14. Considere o ponto ( x , y ) que está no gráfico de y = x - 3 . Sendo L a distância entre os pontos x , y e ( 4,0 ) , represente L em função de x .

Passo 1

O primeiro passo vai ser olhar a coisa de forma mais gráfica. Pra começar, vamos desenhar y = f x = x - 3 :

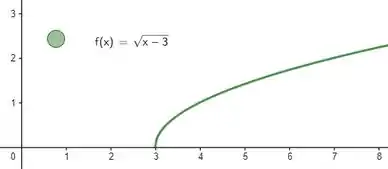
Agora podemos marcar os dois pontos cuja distância queremos saber. O primeiro é o ponto 0,4 e o segundo é o ponto P = x , y que está sobre a curva. Como y = x - 3 , para qualquer x , as coordenadas de P serão P = x , x - 3 :

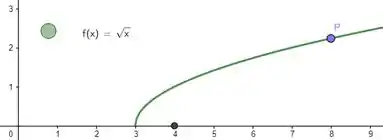
Pra fechar, só ligar um ponto ao outro e achamos L .

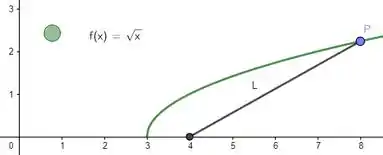
Passo 2

Perceba que se projetarmos o ponto P pro eixo O x , acabamos montando um triângulo retângulo, cuja altura é exatamente a altura y do ponto P :

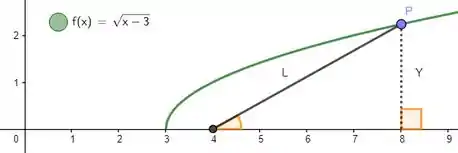
Agora nota o seguinte galera, o ponto P tem coordenada x , y não tem? Então podemos dizer que a reta vermelha abaixo tem tamanho x :

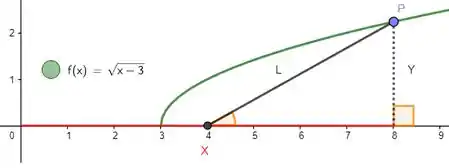
Como x é maior do que a base do retângulo, que só começa mesmo no ponto 0,4 , subtraímos 4 unidades de x e achamos:

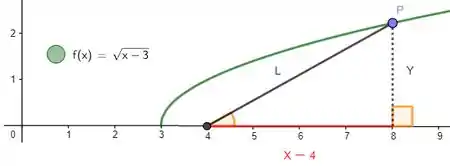
Podemos observar que não importa que ponto que a gente escolha um dos catetos será y e o outro será x - 4 . Fazendo Pitágoras, achamos

L 2 = x - 4 2 + y 2

L 2 = x 2 - 8 x + 16 + x - 3 2

L 2 = x 2 - 8 x + 16 + x - 3

L 2 = x 2 - 7 x + 13

L x = x 2 - 7 x + 13

Resposta

L x = x 2 - 7 x + 13

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a distância entre os pontos dados.(0,2) e (0,3)
Calcule a distância entre os pontos dados.(- 1,2) e (0,1)
Calcule a distância entre os pontos dados.(1,1) e (2,2)
x , y é um ponto do plano cuja soma das distâncias a - 1,0 e 1,0 é igual a 4 .Verifique que x 2 4 + y 2 3 = 1 Supondo y ≥ 0 , expresse y em função de x e esboce o gráfico da função obtida.
Calcule a distância entre os pontos dados.(1,2) e (2,3)