Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.3 - Ex. 21

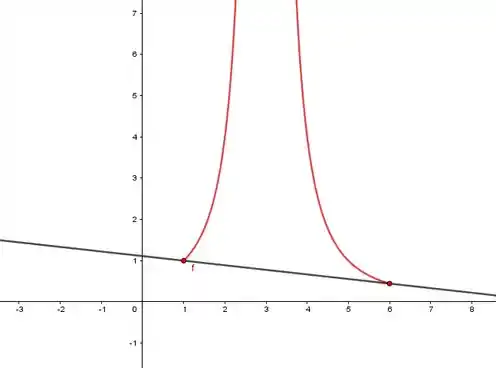
Determine qual das hipóteses do teorema do valor médio não é satisfeita. Faça um esboço do gráfico de y = f ( x ) e da reta que passa pelos pontos a ,   f a e b ,   f b .

f x = 4 x - 3 2 ; a = 1 ,   b = 6

Passo 1

Como f é um quociente, é preciso garantir que seu denominador seja sempre diferente de zero. Assim:

x - 3 2 ≠ 0 ⇒

x - 3 ≠ 0 ⇒

x ≠ 3

Note que quando x = 3 a função f não existe. Como 3 ∈ [ 1 ,   6 ] temos que f não é contínua neste intervalo. Consequentemente, f não é derivável em ( 1 ,   6 ) .

Passo 2

Vamos observar o comportamento de f no extremo do intervalo [ 1 ,   6 ] .

→ x = 1 :

f 1 = 4 1 - 3 2 ⇒

f 1 = 4 - 2 2 ⇒

f 1 = 4 4 ⇒

f 1 = 1

→ x = 6 :

f 6 = 4 6 - 3 2 ⇒

f 6 = 4 3 2 ⇒

f 6 = 4 9

Observe também que f terá um comportamento assintótico quando x se aproximar de 3, pois o numerador permanecerá 4 e o denominador aproximará de zero.

Passo 3

Vamos determinar a equação da reta que passa por ( 1 ,   1 ) e 6 , 4 9 . Seja m a inclinação desta reta, temos:

m = 4 9 - 1 6 - 1 ⇒

m = 4 - 9 9 5 ⇒

m = - 5 9 5 ⇒

m = - 5 9 . 1 5 ⇒

m = - 1 9

Logo a equação da reta será:

y - 1 = - 1 9 x - 1 ⇒

y - 1 = - x 9 + 1 9 ⇒

y = - x 9 + 1 9 + 1 ⇒

y = - x 9 + 10 9

Resposta

Logo, f x = 4 x - 3 2 restrita ao intervalo [ 1 ,   6 ] não satisfaz as duas hipóteses do teorema do valor médio (não é continua nem derivável). Esboço do gráfico de f e da reta que passa por ( 1 ,   1 ) e 6 , 4 9 :

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça um esboço do gráfico da função no intervalo indicado;Teste as três condições (i), (ii) e (iii) das hipóteses do teorema de Rolle e determine quais entre elas são satisfeitas;Se as três condições
Determine qual das hipóteses do teorema do valor médio não é satisfeita. Faça um esboço do gráfico de y = f ( x ) e da reta que passa pelos pontos a ,f a e b ,f b . f x = 3 x - 4 2 3 ,a = - 4 ,b = 5
A interpretação geométrica do teorema do valor médio é que para um valor adequado de c no intervalo aberto ( a ,b ) , a reta tangente à curva y = f ( x ) no ponto c ,f c é paralela à secante que passa
A interpretação geométrica do teorema do valor médio é que para um valor adequado de c no intervalo aberto ( a ,b ) , a reta tangente à curva y = f ( x ) no ponto c ,f c é paralela à secante que passa